このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
確率問題
17の(1)がわかりません
解説ォお願いします
(追記: 2024年12月8日20:37)
ノートです

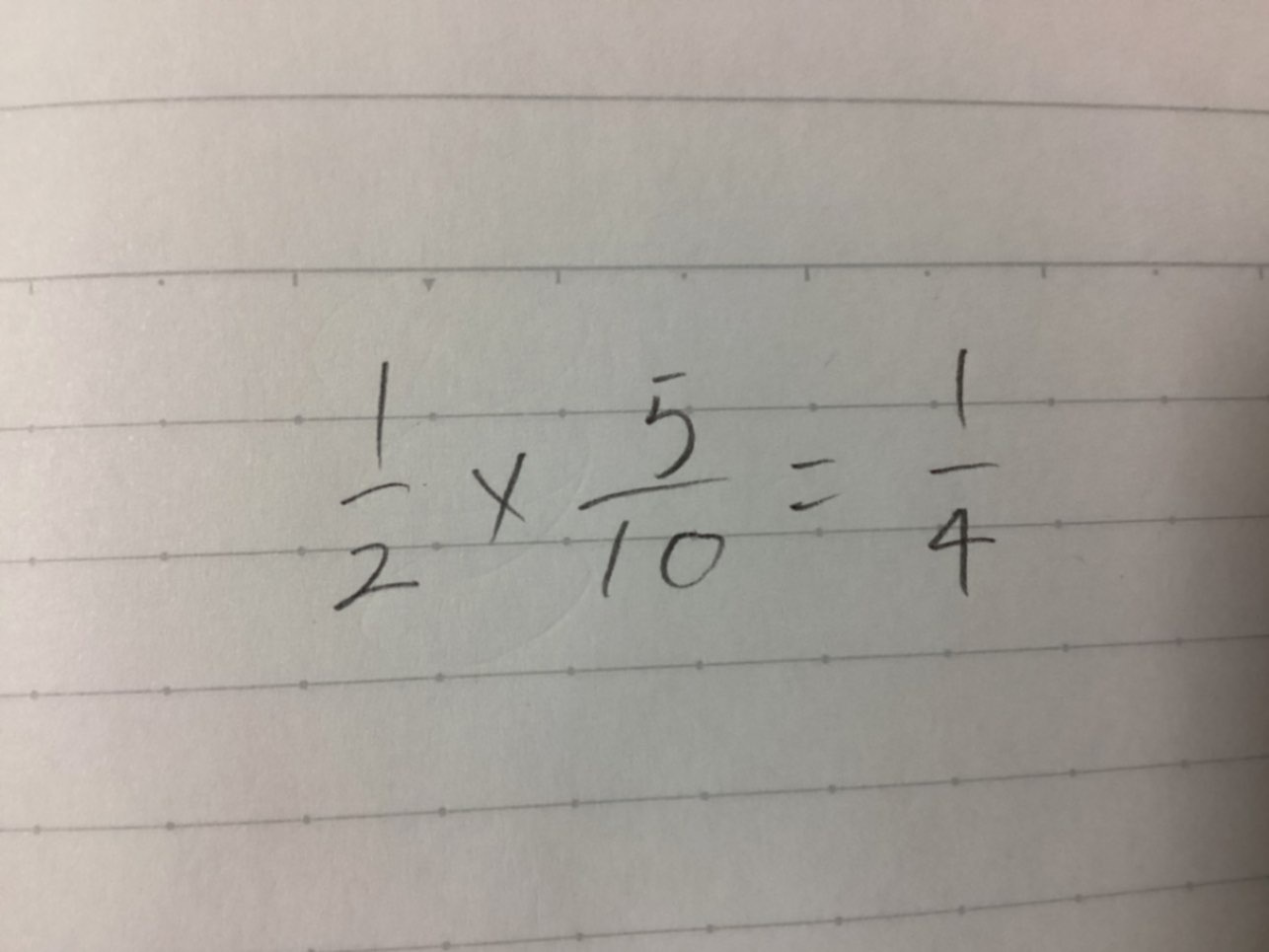
回答
生 卵 さん、こんばんは。初めての方ですね。よろしく。
ここは質問のサイトなので、丸投げは…ちょっと…なんです。
質問の時は、自分ではこう考えたけれど答が合わないとか、ここまでやったんだがその先はどうすればいいのかとか、ヒントをくれとか…
一番いいのは、あなたのノートの写真をアップしてくれることです。次回からはそうしてくださいね。ここでは会話型を目指しています。やりとりしながらわかるまで説明します。解答だけ欲しいのなら他のサイトの方がいいかもしれません。
(1)は条件付確率だということはわかっていますか?そのへんのあなたの状況が分からないと的確なアドバイスができません。
とにかく当たりくじを引きました、という条件の下で、Aを選んで当たりくじを引いた、という確率を求めます。条件付確率の求め方の式は教科書にあるはずです。当てはめてみてください。それでうまくいかないときや、そもそもどう当てはめたらいいのかわからないときや、分母や分子に来る確率が求められないとか言ってください。質問の方を編集してもいいし、コメント欄に書いてくれてもいいです。
じゃ、なにかの反応をお待ちしていますよ!がんばりましょう!
(追記: 2024年12月8日21:27)
コメント、拝見しました。
あなたの書いた式は「Aを選んであたりを引く」確率ですね。条件付確率ではそれが分子に来ます。
条件付き確率の求め方
事象Xが起こったという条件での事象Yが起こる確率= $\dfrac{(事象XとYが同時に起こる確率)}{(事象Xが起こる確率)}$
で求められます。このへんは教科書の説明を読んでくださいね。
今の問題では事象Xは「1人目の人が当たる」ことです。事象Yは「1人目の人が箱Aを選んで当たりくじを引く」ことです。
あなたの計算で求めた $\dfrac{1}{4}$ は事象Yの確率です。
事象Xのほうは、Aを選んで当たったかBを選んで当たったか、ですから
$\dfrac{1}{2}\times\dfrac{5}{10}+\dfrac{1}{2}\times\dfrac{3}{10}=\dfrac{2}{5}$
となります。
よって求める条件付確率は
$\dfrac{\dfrac{1}{4}}{\dfrac{2}{5}}=\dfrac{5}{8}$
となりますよ。
これで大丈夫ですか?まだわからない点があれば、コメント欄に書いてください。
(追記: 2024年12月8日21:31)
この問題の場合では、事象Yが事象Xの一部分なので、「XとYが同時に起こる」といっても実はYが起こることと同じです。だからちょっと違和感があるかもしれませんね。
丸投げしてしまってすいません💦 始めてやった時にはノートのようになったんですけど 答えが8分の5になるらしいので、どうやったらその答えになるのかが知りたいです 条件付き確率はわかるのですがどうやって使うのかがわかりません😓
追記したので読んでください。
ありがとうございます!理解できました! 事象Xの場合を忘れていました😓
理解できたのならよかったです。書いた甲斐がありました。またどうぞ。