メネラウスの定理

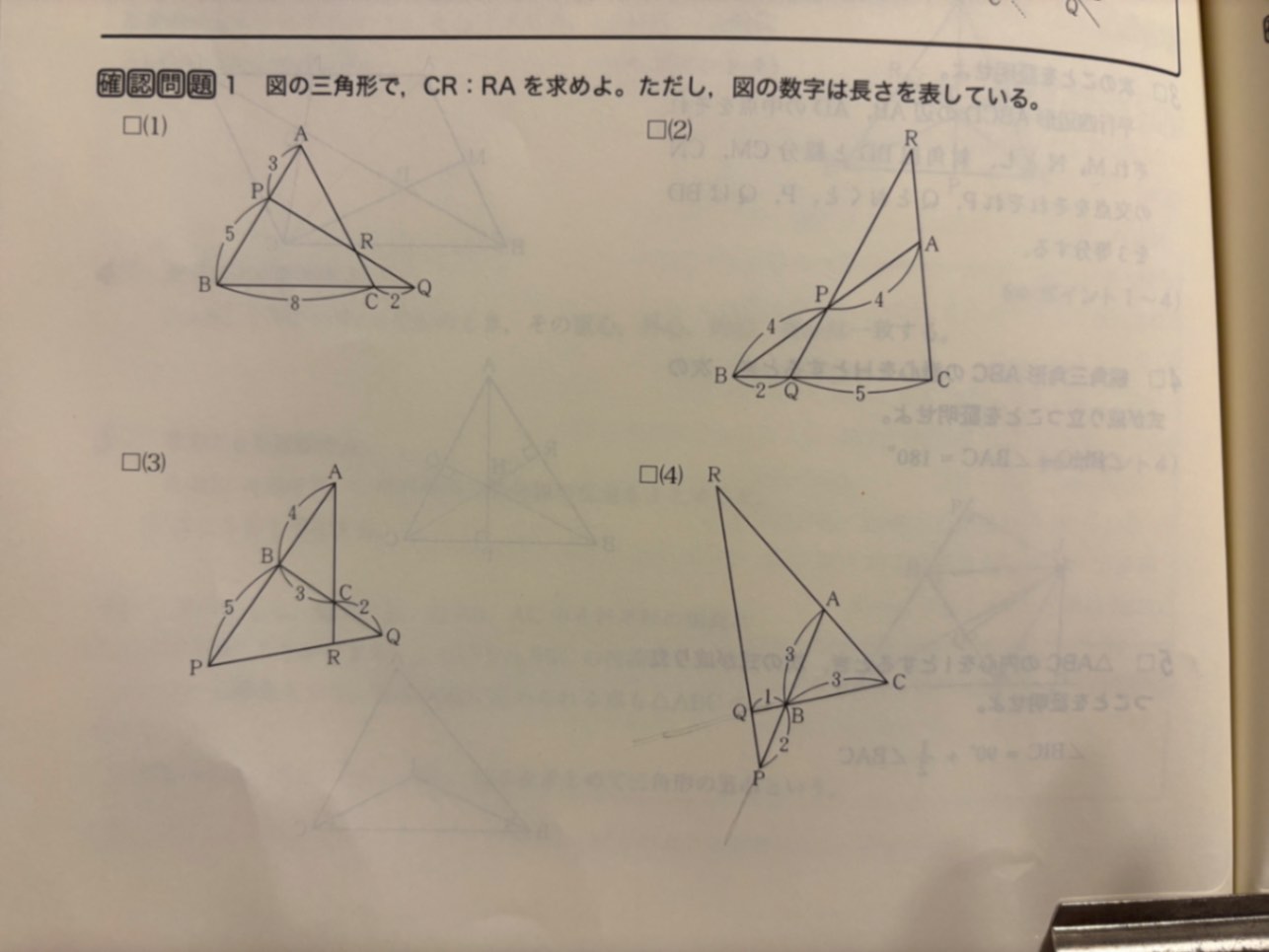
（4）の問題についてです。 与えられた情報からどのように攻めれば解を求められるのか、が分かりませんでした。 解説お願いします。 【追記】 メネラウスの定理の証明の解説があるのですが、（写真2枚目） BQ ：QC＝BP：PD,CR：RA＝DP：PA 上記の関係がなぜ成り立つのかが分かりませんでした。 ご教示くださると嬉しいです。 ［写真］ ・1枚目→問題 ・2枚目→【追記】についての追加写真

ひなた さん、こんにちは。 メネラウスの定理の応用編ですね。 （３）も応用編ですが、そっちは大丈夫だったのですね。 メネラウスの定理をある三角形に適用するときは、辺あるいはその延長上の点を見つけ、辺とペアにします。 この問題では分かりやすいように、元の三角形は△ABCで、辺ABに対して、AB上またはABの延長上に交点Pがあり、CBまたはBCの延長上に交点Qがあり、辺CAまたはその延長上に交点Rを取っています。ABとP、BCとQ、CAとRが組になります。そして、メネラウスの一般の形では、三角形の1つの頂点からはじめて、頂点交点頂点交点…と順にたどって、分数を作っていけば＝１が成り立ちます。証明は厄介ですので、基本の形の証明がわかっていればいいと思います。証明の理屈は同じなのです。 この確認問題１では、メネラウスの定理が使いやすいように、点の名前の付け方が４つとも同じになっていて、どの問題でも AP,PB,BQ,QC,CR,RCの順に分数式を作ればいいようになってます。 $\dfrac{AP}{PB}\cdot \dfrac{BQ}{QC}\cdot\dfrac{CR}{RA}=1$ が成り立ちます。 これで大丈夫ですか？これを読んだら、わかったとか、まだこのへんがわからないから説明してほしいとか、コメント欄になにか返事を書いてください。よろしく。