このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
漸化式について
見ずらい写真で申し訳ありません。
写真1枚目が問題。2と3番目が答えです。
三角の目印が書いてある前までは理解できましたがそこから先がよく分かりません。
・なぜ変形する必要があるのか
・なぜ初項が2であるとわかるのか
このふたつについてお聞きしたいです。
よろしくお願いします。
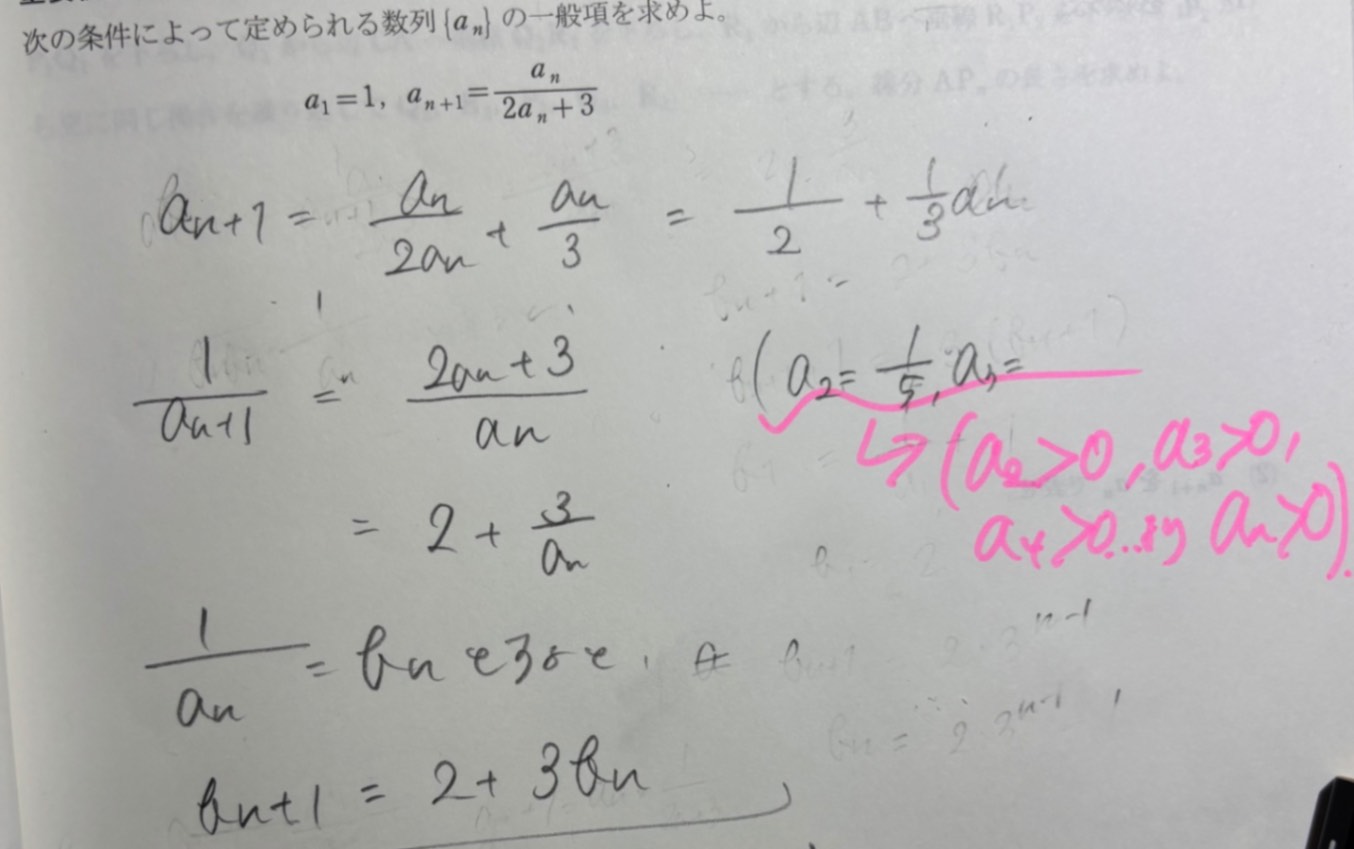


回答
なんだ そう さん、こんにちは。
「初項が2」というのは勘違いですね。
変形したら $b_{n+1}=2+3b_n$ になりましたが、先頭に2があるので初項と勘違いを下のかも。
順番を変えて $b_{n+1}=3b_n+2$ にすれば、これは数列bnの普通の漸化式です。初項が2だと言っているのではありません。
なぜ変形する必要があるのか…どこの変形のことなのかはっきりしませんが…
①逆数を取るという変形は、分数の形の漸化式では定石の一つです。いつでもうまくいくというやり方ではないですが、このように逆数を取るとうまくいくことがあるので「なぜ変形する必要があるのか」ではなく、「こうやるとうまくいく」からやるのです。
②bnの漸化式を、その下のように変形するところかな?
これも「このように変形すると等比数列が現れて解ける!」からやるので、必要があってやるわけではありません。
本来は「なんとか等比数列の形に変形したいなぁ」という欲求から生まれた解法です。
この変形自体の作り方は大丈夫なんですか?右の方にcを使って書いてある「特性方程式」は大丈夫ですか?
コメント欄になにか返事を書いてください。
お答えいただきありがとうございます わからなかった変形はbnの漸化式を変形するところです。説明不足ですみません。 等比数列を見やすくするための変形なのですね 特性方程式、は よくわかっていないです…
漸化式を解くうえで、特性方程式はとても大切です。2項間漸化式、3項間漸化式の特性方程式があります。ネットで検索すれば解説がいっぱい出てきますよ。https://manabitimes.jp/math/1299 なんかがいいかも。
わざわざありがとうございます 理解できました テストで解けるように演習頑張ります
がんばって下さい!
「なぜ初項が2であるとわかるのか」についてです。
解答では、$3$ つの数列 $\{a_n\}, \{b_n\}, \{b_n+1\}$ が扱われています。質問文では、どの数列について質問しているかが省略されていますが、文脈から判断すると $\{b_n+1\}$ の初項についての質問と推測します。
初項とは、数列の $1$ 番目の項のことです。そのため、$\{b_n+1\}$ の初項は $n=1$ を代入して求められる $b_1+1$ です。$3$ 枚目の写真の $4$ 行目に、$b_1+1$ がどのように計算されて $2$ になるかが示されています。
n=1のときを当てはめてあげれば良かったのですね、 見落としてました。 お答えいただきありがとうございます。 助かりました。