このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
三角関数
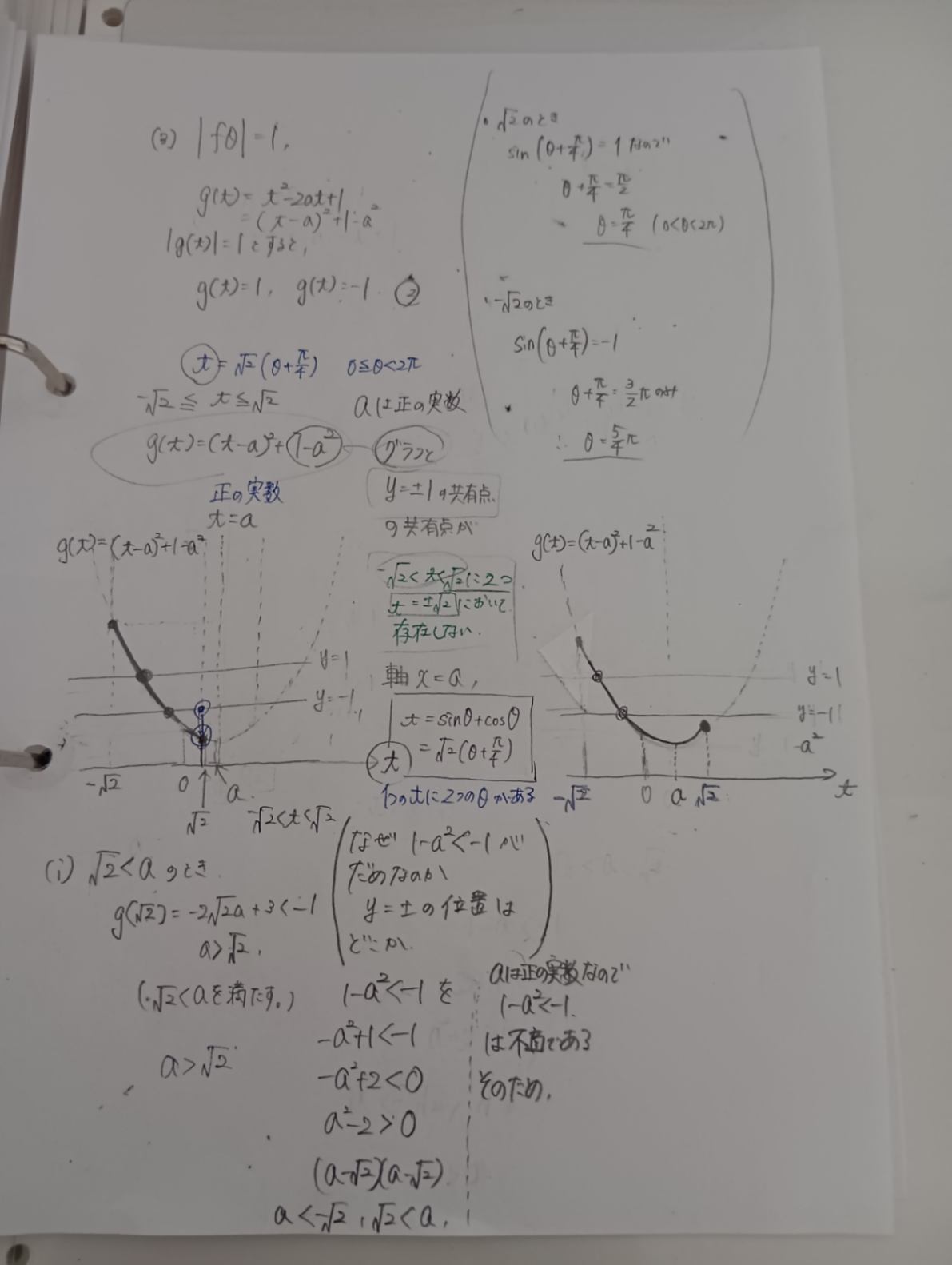
(3)の0<a<√2の部分で引っかかります。
(1)(2)は、わかりました。
私のノートと模範解答ではyの位置がなぜ私のノートと比べて下にあるのかがわかりません。


回答
杉 山 さん、こんにちは。初めての方ですね。よろしく。
さて、あなたの質問が何なのかはっきりわかりません。
「(3)の0<a<√2の部分で引っかかります。」…どのように引っかかっているのですか?
「(3)の0<a<√2の部分」って模範解答の場合分け(i)ですか?このように場合分けをすることが分からないということでしょうか?
「yの位置が」…??y=1とかy=-1とかの直線の位置関係かな?模範解答の図と比較しているのはあなたの図のどちら?
あなたがアップしてくれたノートはそこまでで止まっているのかな?その先があるのかな?
最後のところは場合分けをしているのかな?左端にカッコがちょっと見えるので。「のとき」もあるし。でもその右の0<a≦√2はなに?場合分けの片割れ?
あと、質問の際はあなたが持っている情報はなるべくなら全部見せてほしいのです。あなたのノートも模範解答も一部だけなので、g(t)とかの由来も心配です。模範解答と、せめて(3)の部分のノートは全部見せてください。
質問のページの編集ボタンで質問文の編集や写真の追加のアップもできます。お待ちしています。
ここでは会話型を目指しています。やりとりしながらアドバイスできるところはしていきます。
================
追記
あなたのと模範解答では(i)(ii)が逆なのでどちらを聞かれているのか分からないのですが…
模範解答の(i)のほうでは頂点のy座標ーa²+1がー1より大きいので直線y=-1と交わることはないですね。y=1とー√2と√2の間の2点で交わりたいのですが、aの値にかかわらずt=0で交わっていますので、あとは軸より右でt=√2より小さいとことで交わることが条件になります。
模範解答の(ii)のほうは、軸が範囲の√2の右になってしまうので、じくより右で交点があってもしょうがないのです。よって軸より左で2つの交点があるとすれば、それは2直線のそれぞれと交わらなければならないということです。
なかなかことばでの説明は難しいですが、これで大丈夫ですか?まだこのへんがわからないから説明してほしいとか、コメント欄に書いてください。
私の味方になってくれて嬉しいです。 y=±1の直線の位置関係がわかりません。手書きが私の解答で、画面を撮ってるのが模範解答です。√2<aの部分は場合分けの前半で、0<a≪√2は場合分けの後半です。 前半は理解できたので、おいておきました。 aは正の実数なのでこの分け方てあってるとおもいます。 模範解答も載せます。
画像5つしかあげられないんですね。消してからあげました。 グラフ(-√2<t<√2)とy=±1の交点が2つであればθの値が4つになるのは分かったのですが。2つの交点は私がノートに書いたverもあるのでは?なんでこれはだめなの?って思いました
で、あなたの質問は具体的に何なのでしょうか? y=±1の直線の位置関係ということでしょうか? あれ、あなたのノートは消さないで下さい。復活してくれないと回答のしようがありません。
質問は、 模範解答では、y=-1が2次関数の頂点の下にあって交点がなくy=1と2次関数との頂点がふたつですが、 ノートにあるようにy=±1で、それぞれ一つ合計2つあるのは、何故だめなのか でした。 考えてみたんですけど、aが正の実数だからかなと思い、ノートに加筆してみました。
aが正の実数だからとかではなく、グラフの軸と√2の位置関係で決まってきます。上の回答に追記しましたので、読んでください。