三角関数のグラフ

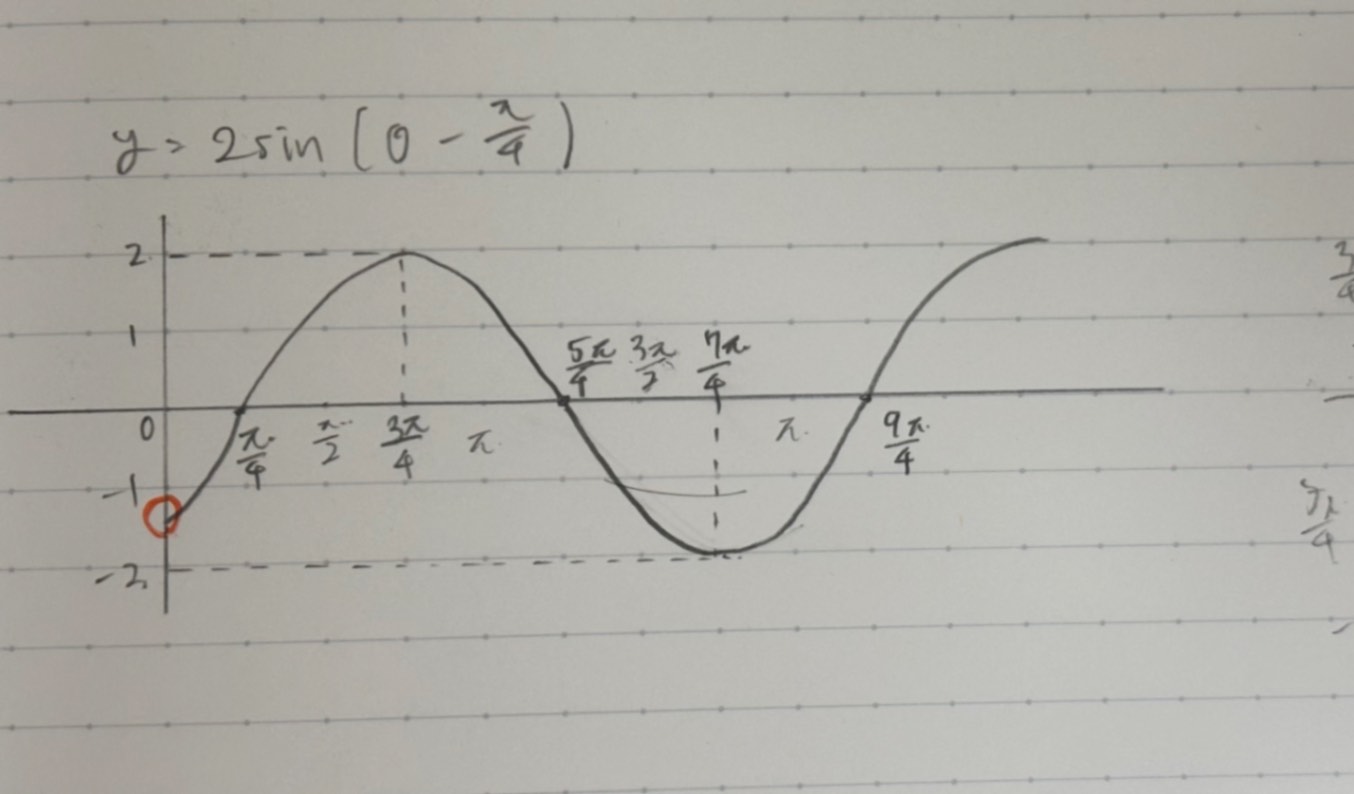
sinやcosのグラフを並行移動させたときのグラフが始まる値の求め方を教えていただきたいです。 例えば$y = 2\sin\left( \theta - \frac{\pi}{4} \right)$のグラフは写真のようになると思うのですが、オレンジのペンで丸をした交点の値はどうやって求めるのでしょうか。 $sin\frac{\pi}{4}$なので$\frac{\sqrt{2}}{2}$になるのではないかと思ったのですが、グラフを見る感じ違うような気がして質問させていただきました。

θに0を代入すると2sin(ーπ/4)となります。sin(ーπ/4)はsin(7π/4)となり、-1/√2となります。 最後、この数字を2倍することで2sin(θ-π/4)でθが0の時の値を求めることができます。 語彙力がなく申し訳ありません。