このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
青チャート



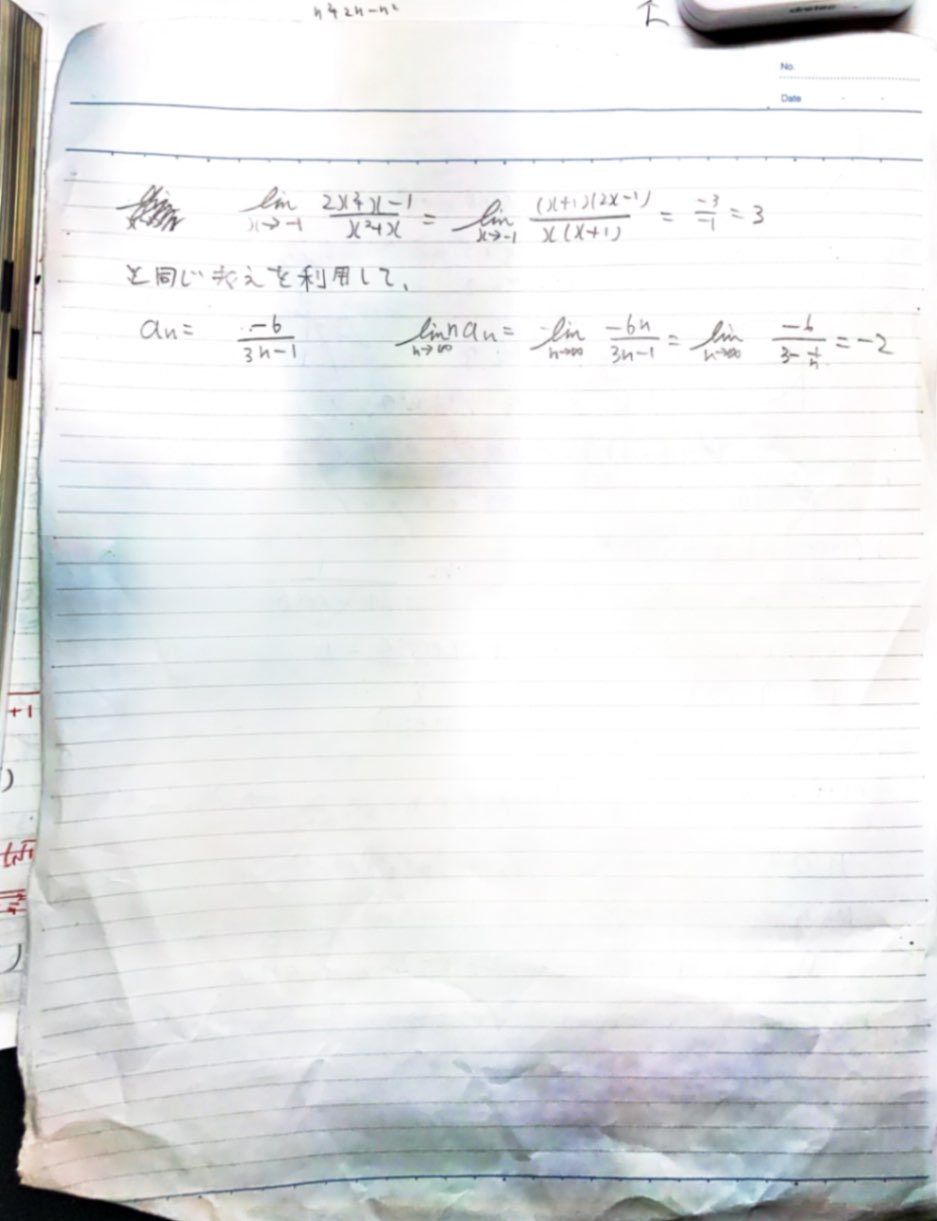
回答
左側と右側にある時を合わして、考えているのにr=+-e(aーrcosθ)としたら、左側と右側に来るためのそれぞれのRまとシータの条件を無視していることになりませんか? また、原点中心半径αの極方程式はr= αと書きますが、これは一般型ではなくないですか?
なるほど、そういう意味ですか。確かに、左にあるときと右にあるときではrとθには条件があります。でもそれはPHが正であるということを立式の段階で2通りに分けていますので、そもそもそのように分けたことが左右の条件になっています。だから大丈夫だと思いますよ。 「原点中心半径αの極方程式はr= αと書きますが、これは一般型ではなくないですか?」これはどういう意味の質問ですか?もう少し書いてください。一般形?原点中心半径αの極方程式はr= αとしか書きようがないですね。
「2次曲線の一般の形は習っているはずですね。この答の式しかなかったはずです。」と仰いましたが一般型とはなんでしょうか?r(1+echosθ)=lのことでしょうか?それが一般型だとしたらr=aは一般型では無くないですかということです。説明が下手ですいません。
あ、一般形という言葉にこだわってますね。ゴメンナサイ。一般形という言葉はあいまいでした。離心率の変化ですべての2次曲線が表せるという意味でr(1+ecosθ)=lあるいは同じことですがr=l/(1+ecosθ)は「2次曲線を一つの形式で表わせるという意味で2次曲線の一般形です」と書きました。r=αは「原点を中心とする円の一般形です。座標で言えばx²+y²=r²は一般形であるのかどうか。一般形なら中心を決めたものではなく(x-a)²+(y-b)²=r²のほうが一般的ですね。そういう意味ではr=αは一般形ではないです。しかし、この言葉にこだわらなくてもいいと思います。言いたかったのは、極座標では円、楕円、放物線、双曲線とも1つの式になり、±とかで区別した2つの式にはならないことは教科書や参考書から読み取っておいた方がいいということです。こちらもあなたの疑問点が明確につかめず申し訳なかったです。
なるほど。わざわざありがとうございます。
どういたしまして。
もう一つお願いします
追記です。よろしくお願いします
ひとつ前の質問なのですが、マイナスで答えが出た後にそれが1つにまとまると毎回確認しなければならないのですか?初見だとどうすればいいのかわかりません。何度もすいませんがよろしくお願いいたします。
19:06のコメントに対して:前にも書きましたが、これは問題を読んだ時点で離心率が出てくるから2次曲線だということがわかり、それなら答の式が2つ出てはこないだろうという予想が立つのです、というか、立ててほしいのです。その上で、結果の式が複数出てきたら、似ている形なら(r、θ)と(-r、θ+π)が同じ点になることを考慮すればたいていは1つになります。それは受験数学の技術として身につけた方がいいです。 19:02のコメントに対して:追記は読みましたが、どれを点検すればいいのかな?
答案の写真、拝見。それは初めから間違いです。n→∞にしたとき、やっと=6になるので、有限のn番目の項はイコールにはなりませんよ。
自分は極限の不定形について本質を理解していないように感じます。不定形とは何なんですか?このままでは極限がわからないものと書かれていますが、数学的に何を意味するのかよくわかっていませんlim n→♾️ 3n/2nは∞/∞の不定形で、Nを約分して2分の3にしますが、∞は数ではなく、限りなく大きいものを表すので、2nも3nも限りなく大きいので2分の3にはならないのではないかと思います。しかし、∞は数では無いので答えが1になることもないとと思います。そもそもの∞の概念が抽象的すぎて本質を掴めません。数ではなく、最大の値を示す∞を計算途中で用いて最終的に答えが数字になるのも少し違和感があります。関数の極限を求める際にも、因数分解して互いに約分しますが、それを展開してnに∞を代入すると分子と分母ともに0になることがありますが、分母がゼロになる計算はしてはいけないのではないんですか?詳しい解説よろしくお願いいたします。
直接に無限を扱っているわけではないので、あまり大げさに考えない方がいいと思います。極限をとるということは、まだnは無限大ではなく、有限の値なのですね。ですから極限を取る前の段階で、nは有限の値ですから、2n/3nは普通に約分できるのですよ。2n/3nの分子も分母も無限大ではないのです。 不定形はなんなのかは、ネットで検索してみれば役に立つページが見つかると思います。このコメント欄に書くくらいの量では無理です。一般にはnを大きくしていくと∞/∞や0/0になってしまって極限が求まりにくい形になるものですよ。 極限はあくまでも有限のnを扱っているのです。nがものすごく大きくなったら値は何に近づくのかを調べているのです。 「最大の値を示す∞を計算途中で用いて最終的に答えが数字になる」のに違和感があるとのことですが、無限大を途中で扱ってはいませんからご安心を! これで大丈夫ですか?いろいろ調べてみてください。
わかりました。ありがとうございました。