このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
小学生 図形(相似)
小6保護者です。先日はありがとうございました。
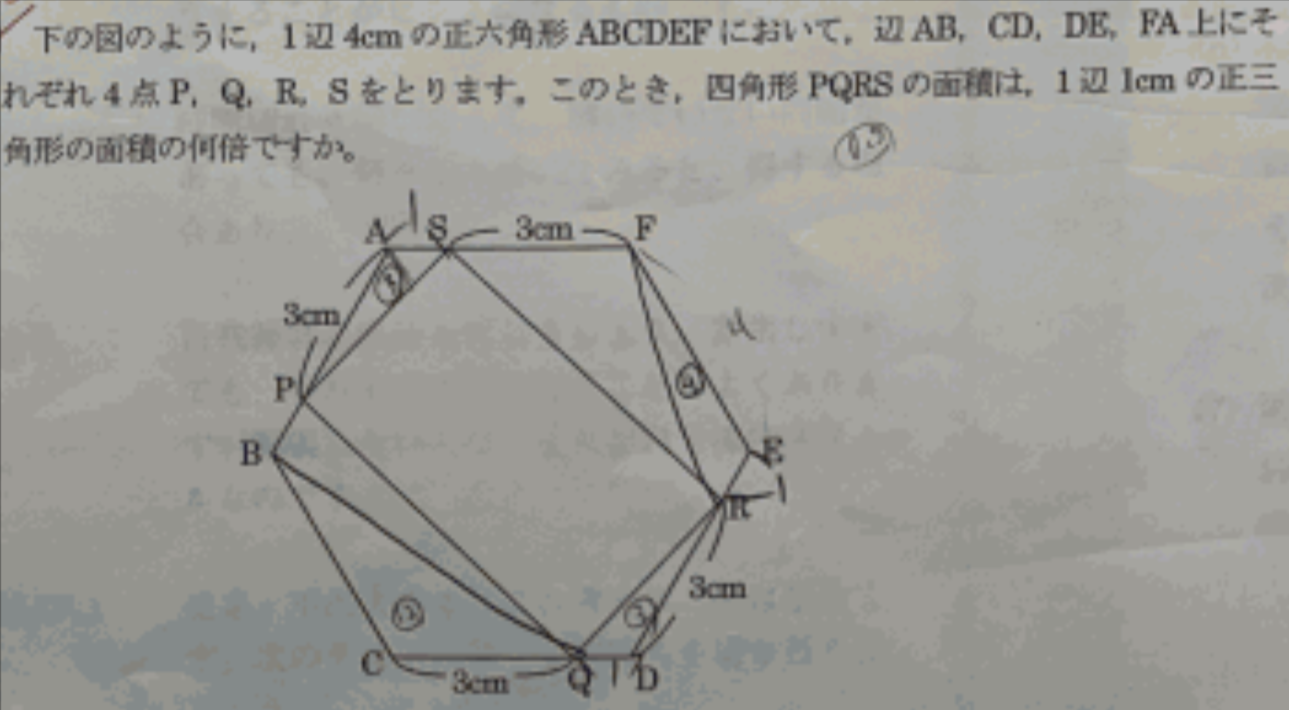
添付の写真の問題で、どうして解答のような式になるのかを教えていただけないでしょうか。
正六角形の周りに延長線をのばして、正三角形を作って考えたりしてみましたが
相似な図形は見つかるものの立式の意味が分かりませんでした。
どうぞよろしくお願いいたします。
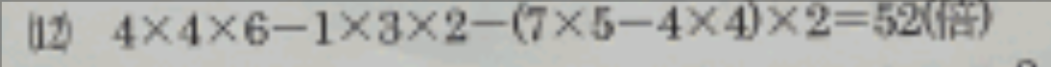
回答
purin さん、こんにちは。
これは実際に出題された問題ですか?
この式の解説をお望みですか?正解に至る考えをお望みでしょうか?
その立式に関してはまだ理解できませんが、ほかの方法で正解が出ますので、それを回答しますね。
まずBC上にBT=3となる点Tをとります。同様にEF上にEU=3となるような点Uを取ります。
1辺が1cmの正三角形の面積を1とするのは気持ち悪いので、ここではSとしておきますよ。
また正6角形の中心をOとします。
方針は全体から余分なものを引いて求めます。
①正6角形の面積は正三角形の相似を使って△ABOは4×4=16で16Sですので(4×4)S×6=96Sです。
②△ABFはひし形ABOFの半分ですから16Sです。
③これをもとに、△ABS=16S×1/4=4S、△APS=△ABS×3/4=3Sと分かります。
図に書き込んであるので、ここまではOKだったのでしょうか。
④T、Uを加えたので△APSと合同な三角形が6個になりました。3S×6=18Sです。
⑤あとは△PTQが分かれば、その2倍を引きますよ。
⑥ここで正6角形PTQRUSに着目します。これが正6角形であることは対称性から認めましょう。説明が必要ならあとで書きますが。
⑦正6角形PTQRUSの面積は96S-18S=78Sで、△PTQはひし形PTQOの半分ですから78S÷6=13S。
⑧△SRUも同じです。
以上より、四角形PQRSの面積は
96S-18S-13S×2=52S となり、52倍が得られます。
1行で式を書けというなら
4×4×6-3×6-13×2=52
です。
ひとつアドバイスですが、難問で解説のない問題を練習として解くことはお勧めできません。その1行の式だけ書かれても得るものはないですね。練習する問題は、詳しい解説があるものでないと意味がありませんよ。ぜひ解説が詳しいものをやるようにしてください。
実は私は、東京の中高一貫超進学校にずっと勤務していたものですが(歳なのでもうとっくに退職)、中学入試の問題を作る担当をしていました。その立場から言うと、この問題も、前回の質問の問題も、小学6年生が解くにはちょっと難しすぎます。大人の数学愛好家とかパズルマニア向けのようで、さすがにこんな問題は作ったことはないです。もしこれがどこかの塾の課題だとしたら、NOT GOODです。お子さんが算数を嫌いになりそうで心配です。あるいは実際に出題された過去問だとしたら、その学校の過去問題集があるでしょうし、それなら解説がたっぷりついているので、ぜひそちらを買うことをお勧めします。
これで大丈夫ですか?
このサイトをご利用になって役に立つのなら、いくらでも聞いてください。
コメント欄になにか返事を書いてください。よろしく。
言葉で説明すると極めて煩雑になるため、$\textrm{3}$ 枚の画像を用いて説明します。
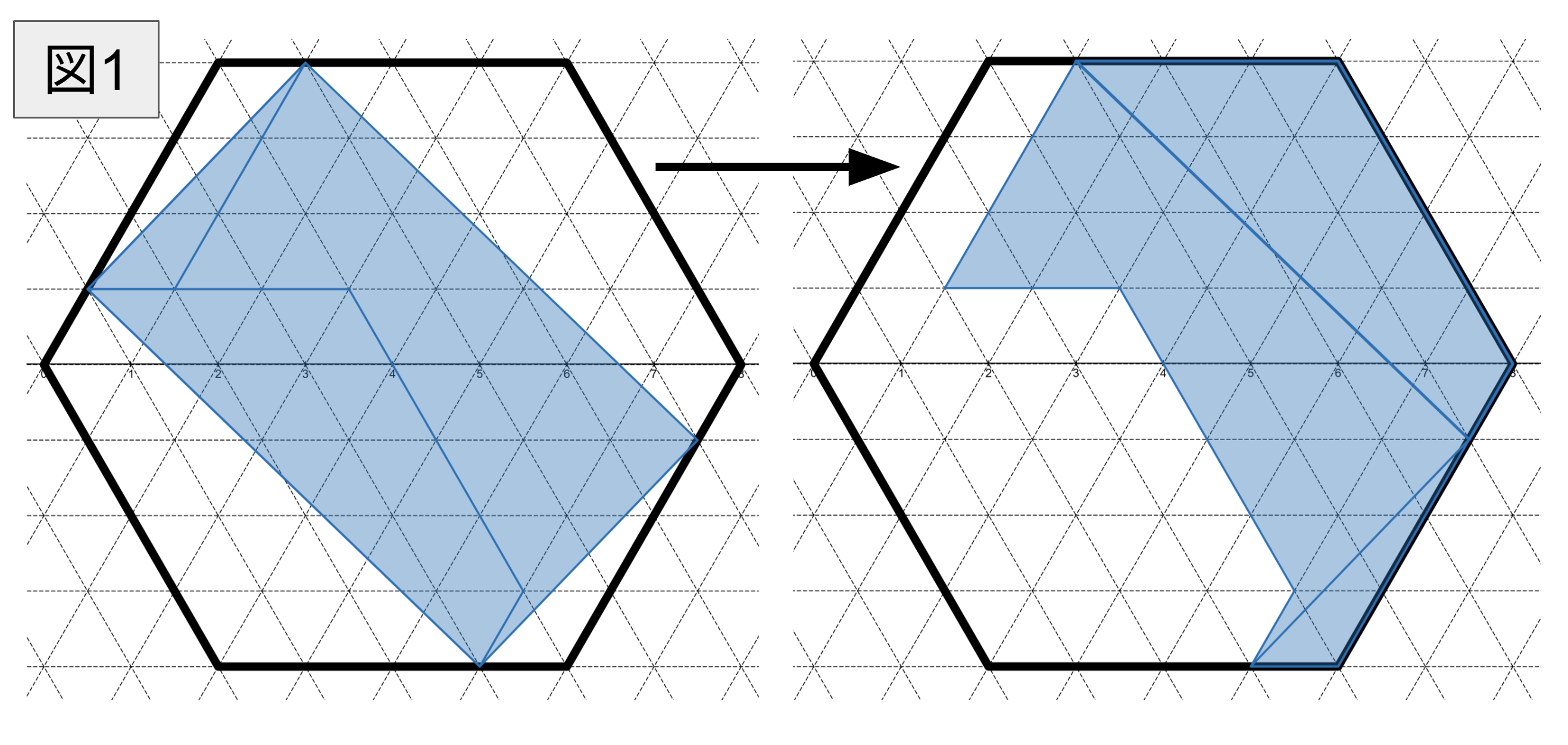
まず、図 $\textrm{1}$ のように四角形 $\mathrm{PQRS}$ を切り貼りします。すると、正三角形を数えるだけの問題になります。一つずつ数えても答えには辿り着けますが、写真の式では工夫して計算されています。
説明のために、一辺が $\mathrm{1} \ \textrm{cm}$ の正三角形を単位正三角形と呼ぶことにします。また、単位正三角形を $2$ 個合わせてできるひし形を単位ひし形と呼ぶことにします。
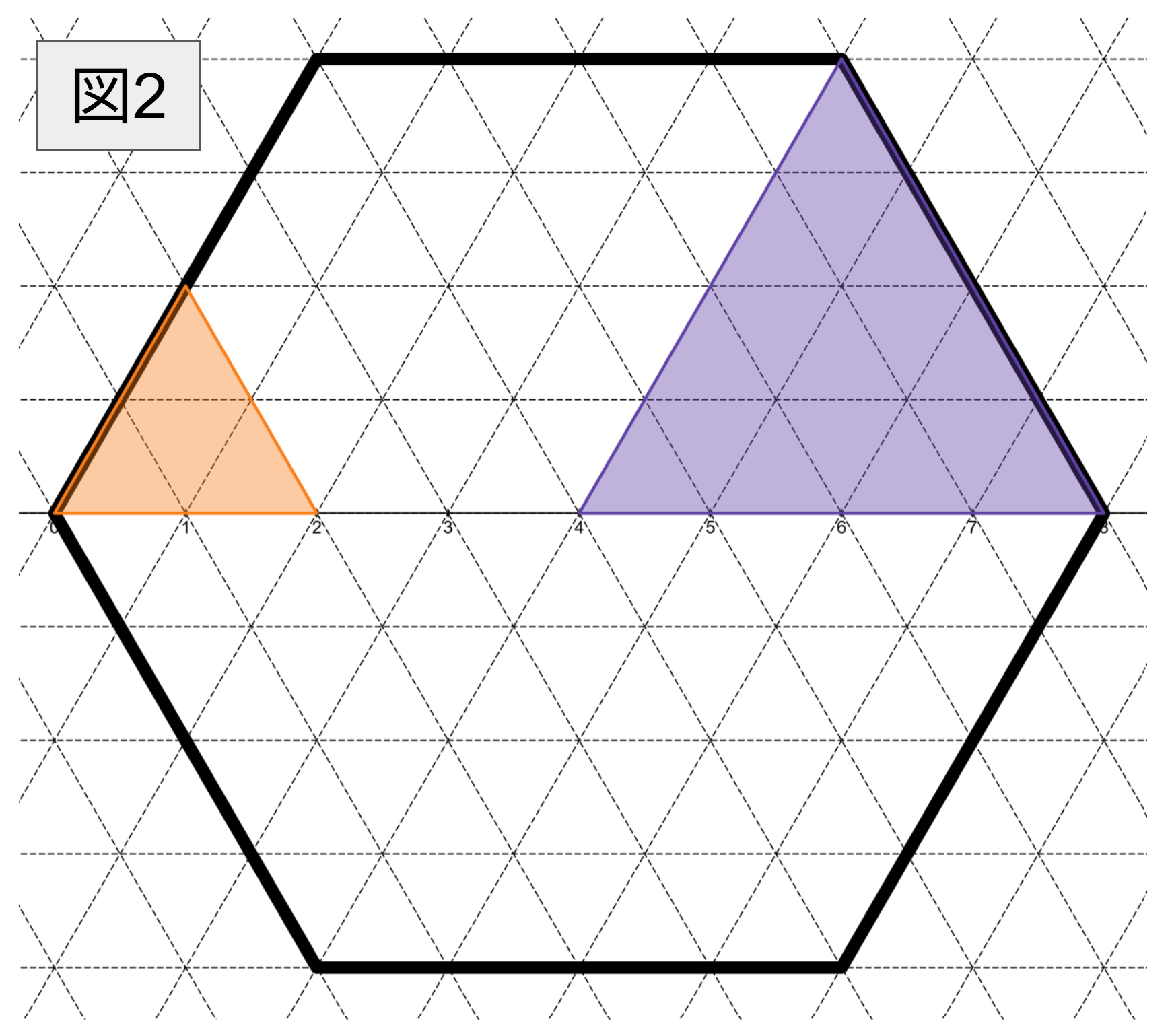
図 $\textrm{2}$ を見てください。橙の正三角形には単位正三角形が $4$ 個敷き詰められていると考えてください。紫の正三角形には橙の正三角形を $4$ 個敷き詰めることができるため、単位正三角形 $4 \times 4 = 16$ 個分です。正六角形 $\mathrm{ABCDEF}$ には紫の正三角形を $6$ 個敷き詰めることができるため、単位正三角形 $16 \times 6 = 96$ 個分です。
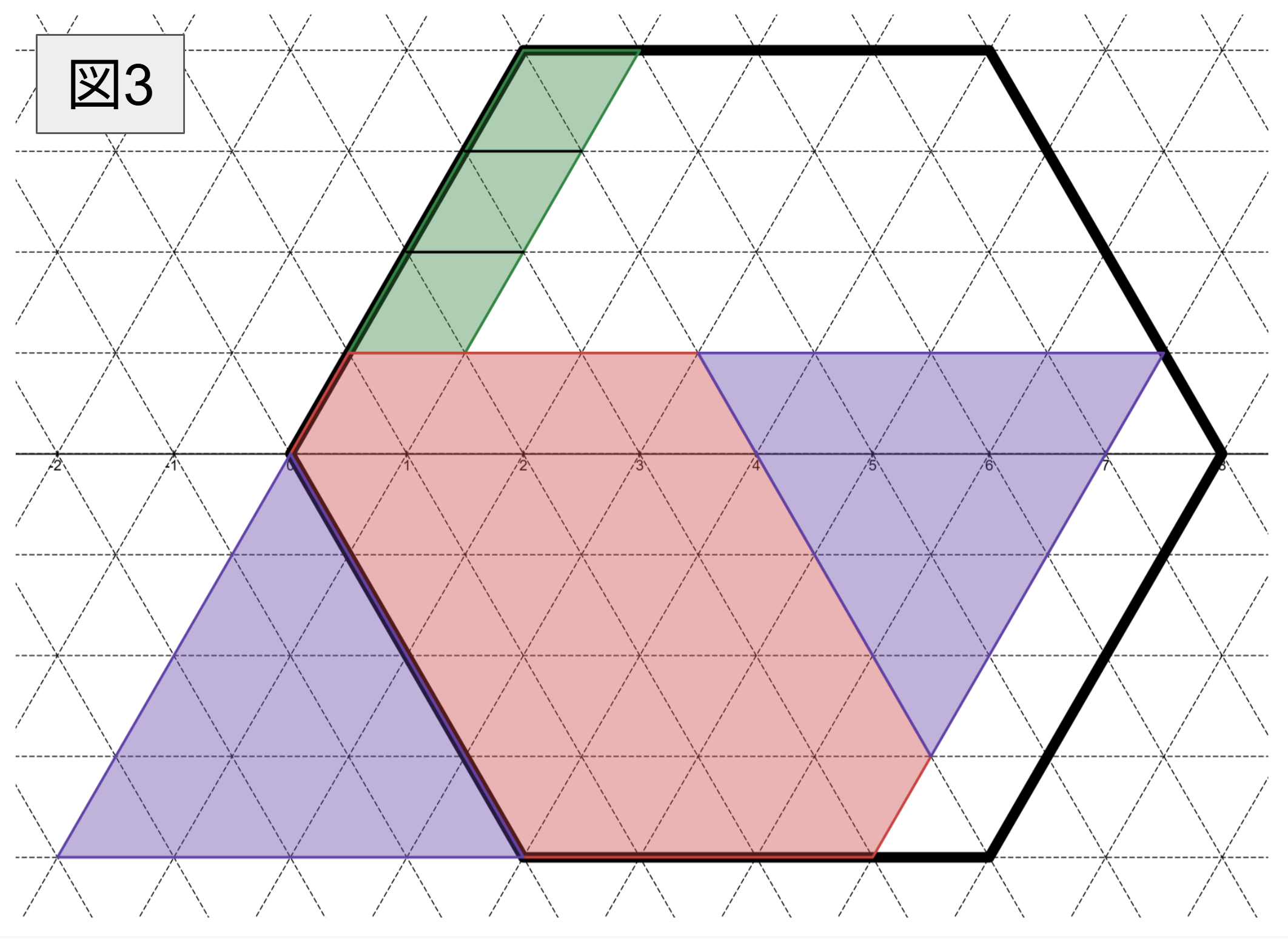
図 $\textrm{3}$ を見てください。緑の平行四辺形には単位ひし形が横に $1$ 個、縦に $3$ 個並んでおり、$1$ 個の単位ひし形には $2$ 個の単位正三角形が敷き詰められています。よって、緑の平行四辺形は単位正三角形 $1 \times 3 \times 2 = 6$ 個分です。
赤の多角形と $2$ 個の紫の三角形を合わせてできる平行四辺形には単位ひし形が横に $7$ 個、縦に $5$ 個並んでいます。$2$ 個の紫の三角形を合わせてできる平行四辺形には単位ひし形が横に $4$ 個、縦に $4$ 個並んでいます。よって、赤の多角形は単位ひし形 $7 \times 5 - 4 \times 4 = 19$ 個分であり、単位正三角形 $19 \times 2 = 38$ 個分です。
最後に正六角形 $\mathrm{ABCDEF}$ から、緑の平行四辺形と赤の多角形を引きます。これにより、四角形 $\mathrm{PQRS}$ が単位正三角形 $96 - 6 - 38 = 52$ 個分であることが分かります。
これらの計算をまとめて書くと、$4 \times 4 \times 6 - 1 \times 3 \times 2 - (7 \times 5 - 4 \times 4) \times 2 = 52$ という式が得られます。