このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
入試対策
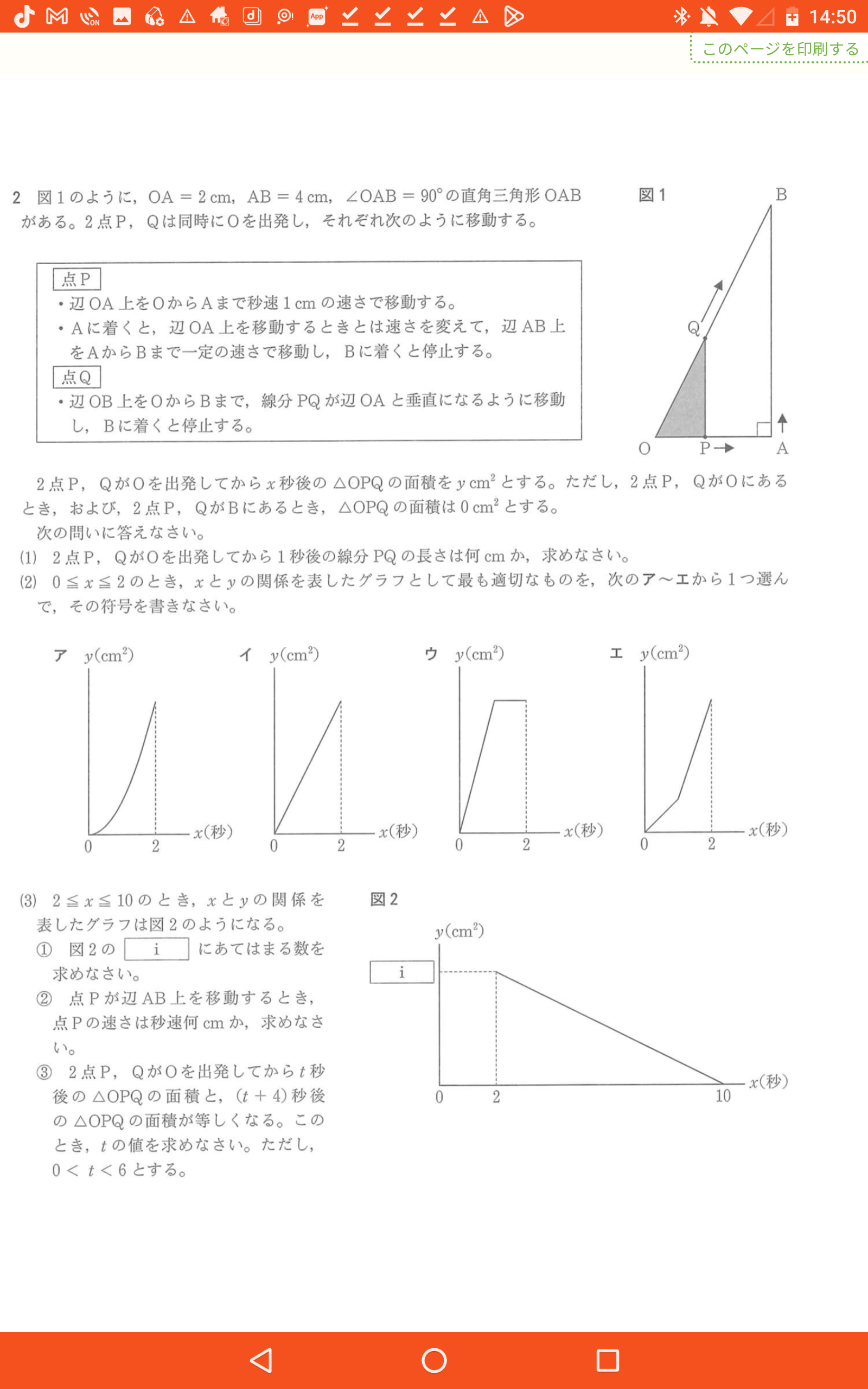
最後の問題についてです。
グラフより面積が一致するには異なる直線での交点でないとできないのでy=2xとy=-1/2x+5にそれぞれx=t、t+4を代入して考えたんですが答えと一致しなくて…
ちなみに答えは3/2です。
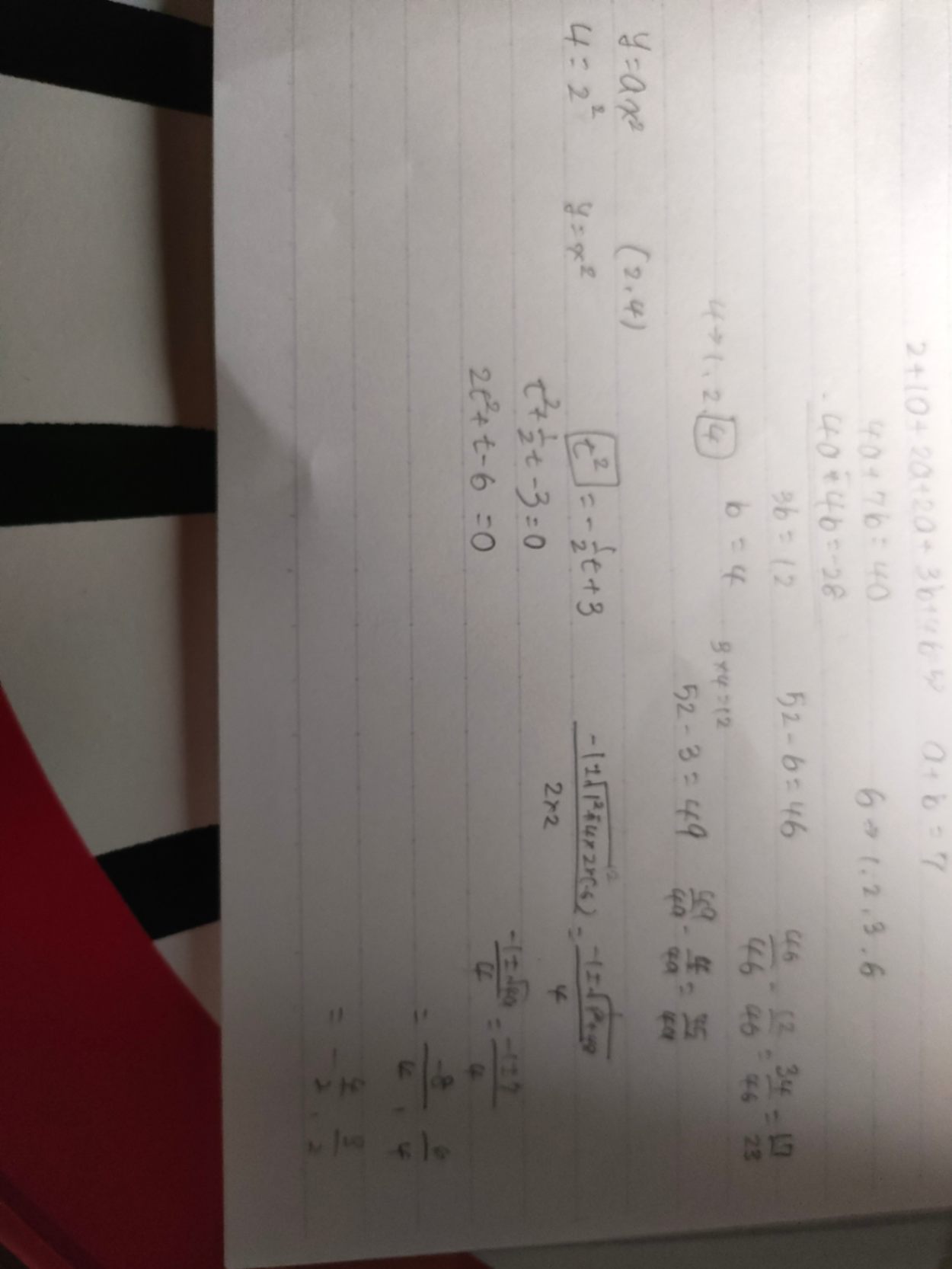
回答
楓さん、こんにちは。
（２）はどれを選んだのでしょうか？答え合わせはしていない？ひょっとしてイのグラフを選んでないですか？
（３）のあなたのノートにｙ＝２ｘっていうのがあって、そこにｔを代入していますが、ｙ＝２ｘではないですよ。つまり（２）のグラフはイではないです。そこから考え直した方がいいですね。
これで、もう少しやってみて、またコメント欄になにか返事を書いてください。お待ちしています。
（2）も間違えて、答えはアでした。 関数y=ax²を使う問題ですか？
関数使って解いてみたらできました。でも（2）はなんであのグラフの形になるかわかりません、底辺の長さと面積は比例しないんですか？
高さが同じなら、三角形の面積は底辺に比例しますが、これは底辺が大きくなると高さも高くなるので、単純に比例というわけにはいきません。底辺の長さがxのとき高さは2xです。三角形の面積はどうなりますか？（2）を考えるときにここまでやらないと答がわかりませんよ。
あーほんとですね。比例にはならないです。 なんとなく分かりました！ありがとうございます。
３枚目の写真見ました。四角で囲ったｔ²ですが、それを出すために横に書いてあるｙ＝ａｘ²とか（２，４）を通るとかは、もう関数が２乗になることを前提にしていますが、それはおかしいです。２３日19:12のコメントに書いたとおり、（２）を考える時に、三角形の面積を式にしますよ。底辺がｘで高さが２ｘだから三角形の面積は1/2ｘ×２ｘ＝ｘ²となり、（２）の答は(ｱ)だと分かります。これを使って（３）では初めから「ｔ²＝…」が書けるのです。わかりますか？