共テ二次関数

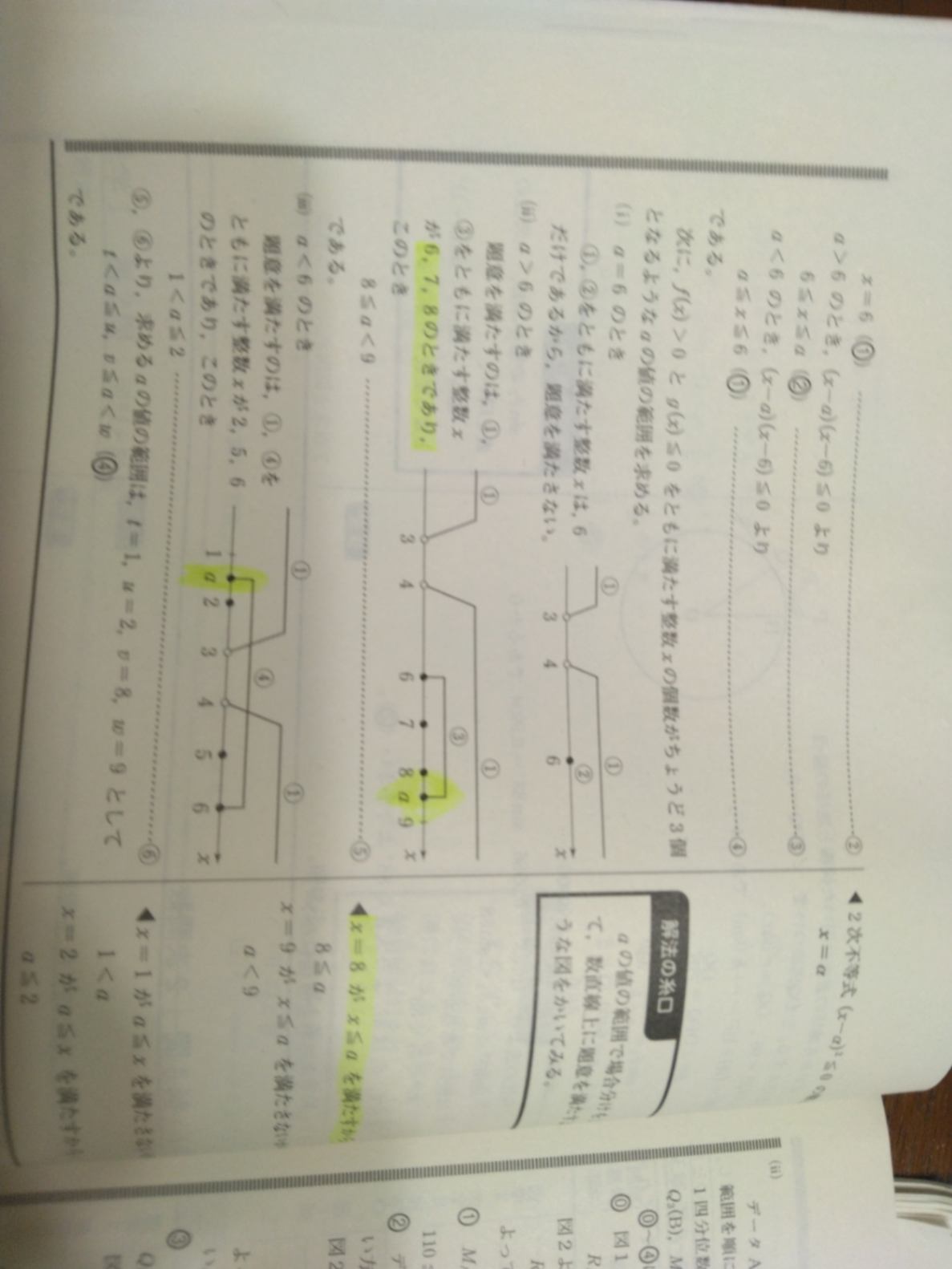
四枚目の解説の黄色いマーカーで引かれている部分がわかりません。問題で言うと【ト】【ナ】【二】です。(ii)(iii)で、なんでAの場所が決まるのかわかりません。右の欄外に「X＝8がX≦Aを満たすから」とありますが、そこもよく理解できません、どこから判断しているのですか？

忠さん、こんにちは。 これは多くの人がつっかえるところです。 (ii)の場合では、数直線で範囲を書いてみると、まず共通の整数として６が入ることが分かります。範囲は６以上ですから、次に７と８が入らなければなりませんので、範囲の終点は７も８も超えます。ちょうどa＝８のときも、そこ（ｘ＝a）は黒丸なのでｘ＝８も共通になり、適します。つまりa≧８が分かります。じゃ、aはどこまで大きくなれるのか？aが９を超えてしまっては、共通な整数が６，７，８，９と4つになるのでダメですからa＜９も確かなことです。、問題なのはaがちょうど９の時です。不等式の解６≦ｘ≦aは両端が黒丸になりますので、もしa＝９の時はｘ＝９も共通な整数になってしまい、不適なのです。よってaは８≦a＜９となります。わかりますか？不等式の解６≦ｘ≦aの右端のaがどの範囲にあれば共通な整数が６，７，８だけになるかを図から読み取ります。 (iii)も同じような考えです。数直線に解を図示してみると、ｘ＝６は共通な整数の最大なものであることが分かります。aの値が小さくなって６から左の方に行くと、ｘ＝５も共通な整数になれます。でもｘ＝４とｘ＝３はそもそもf(x)＞０の解ではないので共通な整数には入れません。aがもっと小さくなってちょうどa＝２になったとき、aのところは黒丸なので両方の解になり、整数解が６，５，２の3個になりました。aはもう少し小さくなって左端が左に移動しても、次の整数ｘ＝１の手前までなら共通な整数は６，５，２ですが、aが１になってしまうとｘ＝１もきょうつうな整数となってしまい、4個になるのでダメ。aが１より小さい場合はもちろんダメ。よって１はだめで２はOK。１＜a≦２となります。 数直線上を端点aが移動していく様子を動画ふうに想像してくださいね。 これで大丈夫ですか？ 欄外のことは、「８も共通になるためには…」ということです。