このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
積分🙇
分母が因数分解形になっているものを部分分数分解しているのですがなぜこのような部分分数分解の組み合わせにしようと思えるのでしょうか?この組み合わせだとA,B,Cのように定数で置けるらしいです。
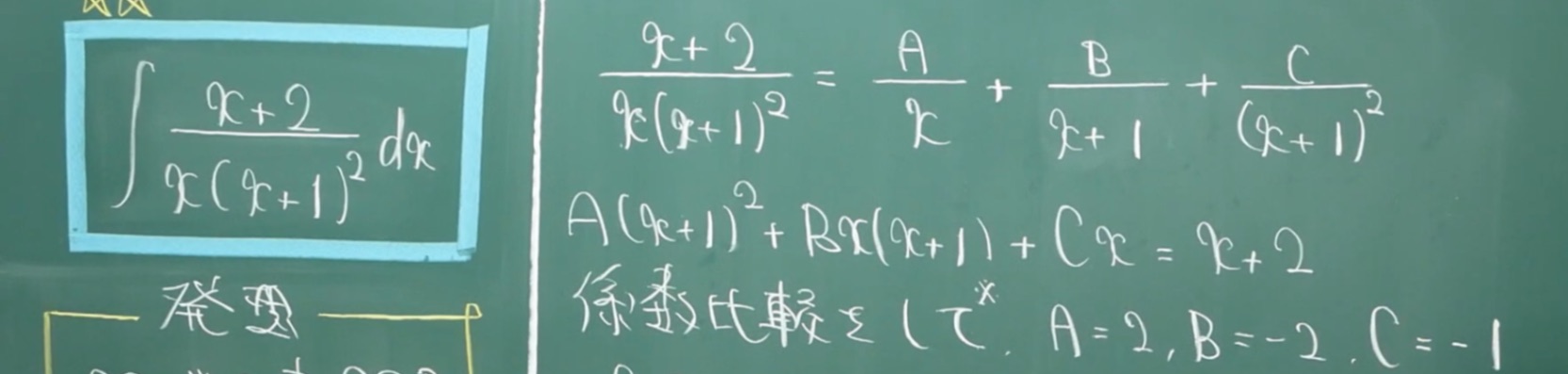
回答
h k さん、こんにちは。
「…しようと思えるのでしょうか」→目的は積分ですから、できるだけ積分計算が楽になるように分解しています。こうすると楽にできるというのは一つの知恵であり、この問題をやったあなたはこの知恵を蓄えておきましょう。
部分分数に分解するのなら、このようにしなくてもいいのです。例えば分母がxの分数と分母が(x+1)²の分数の2つに分解することだってできます。
この場合は、分母が2次式だったら分子は1次式になるので、
$\dfrac{x+2}{x(x+1)^2}=\dfrac{A}{x}+\dfrac{BX+C}{(x+1)^2}$
と置いてから係数比較法でも数値代入法でもいいので、未定の係数A,B,Cを求めるとA=2,B=-2,c=-3 となりますから、
$=\dfrac{2}{x}-\dfrac{2x+3}{(x+1)^2}$
と分解できました。このまま積分することもできます。後ろの分数ではx+1=tという置換積分をすればできます。でも、
$=\dfrac{2}{x}-\dfrac{2x+3}{(x+1)^2}=\dfrac{2}{x}-\dfrac{2(x+1)+1}{(x+1)^2}$
$=\dfrac{2}{x}-\dfrac{2(x+1)}{(x+1)^2}-\dfrac{1}{(x+1)^2}$
$=\dfrac{2}{x}-\dfrac{2}{x+1}-\dfrac{1}{(x+1)^2}$
という変形ができまして、分子は必ず定数にすることができます。
この式なら積分は容易ですね。
それなら最初から、分母がx、x+1、(x+1)²という3つにして、分子をすべて定数だけにするような分解を試みた方が楽です!
もし分母に(x+1)³があったら、それは分母がx+1、(x+1)²、(x+1)³で分子が定数である3つの分数に分解できます。
じゃ、今後は積分で部分分数分解をするときには、あなたもこのような発想をできるようになりましたね!
この緑の板書みたいなのは何ですか?ほんとに板書?
学校とか塾とかの内容だとしたら、まずは担当の先生に質問してみることをお勧めしますよ。ここのように言葉だけではなく、面と向かって、あなたに適した説明をし、図とか指差しとかで教えてくれることでしょう。あれ?左下に「発想」というのがありますね。そこは何が書いてあるのだろうか?知りたいですね。
分かりました。これはYouTubeの動画です。発想は積分するために必要な知識が書かれています。