このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
整数の性質の証明(数学的帰納法)
画像内の↓?と記入した部分の式変形が、どうしてそうなるのか理解できませんでした。
どなたか解説していただけるとありがたいです。よろしくお願いします。

回答
どうにかして13でくくるために、16と3、それから3^k+3をうまく分解して(k+2)乗に統一すれば導けると思います。
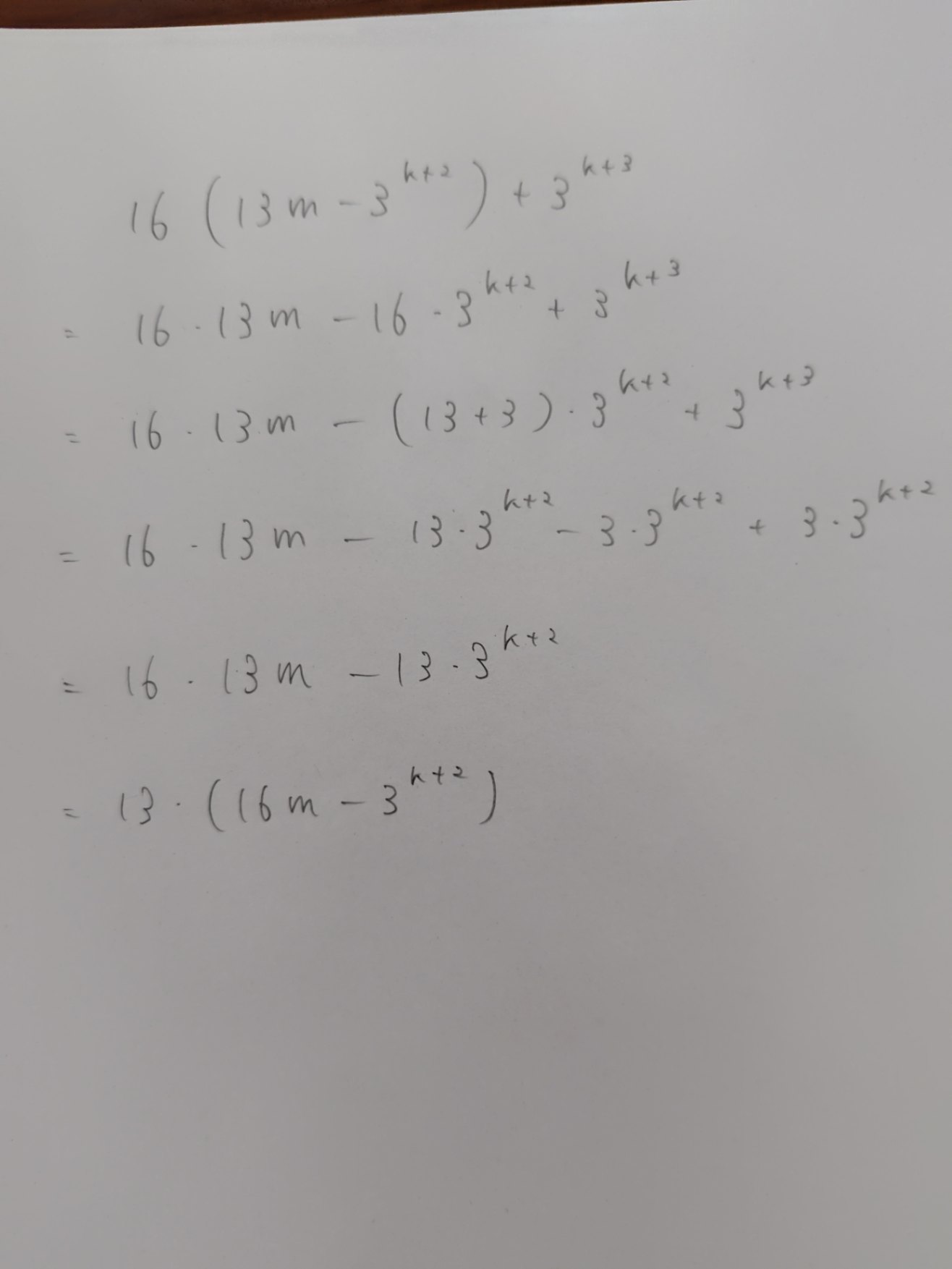
Cocoro さん、こんにちは。はじめてのかたですね。よろしく。
上のわいYさんと、ほぼ同じですが、こんなのでもいけます。
$16(13m-3^{k+2})+3^{k+3}$
3の累乗はk+2の方が低いので、それに合わせます。
累乗をまとめる時の定石です。
$=16\cdot 13m-16\cdot 3^{k+2}+3\cdot 3^{k+2}$
これで累乗の部分が $3^{k+2}$ でまとめられます。
$=16\cdot 13m+(-16+3)\cdot 3^{k+2}$
$=16\cdot 13m-13\cdot 3^{k+2}$
うまいこと13が出てきました!
$=13(16m-3^{k+2})$
これで大丈夫ですか?
ここでは会話型を目指しています。
これを読んだら、わかったとか、まだこのへんがわからないから説明してほしいとか、コメント欄になにか返事を書いてください。よろしく。