このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
三角形の内接円と2辺と接する円
これの18が解けません
ノートを添付しています。そこまでは計算してみましたが値がわからないしあっているかもわかりません。
教えていただけると幸いです
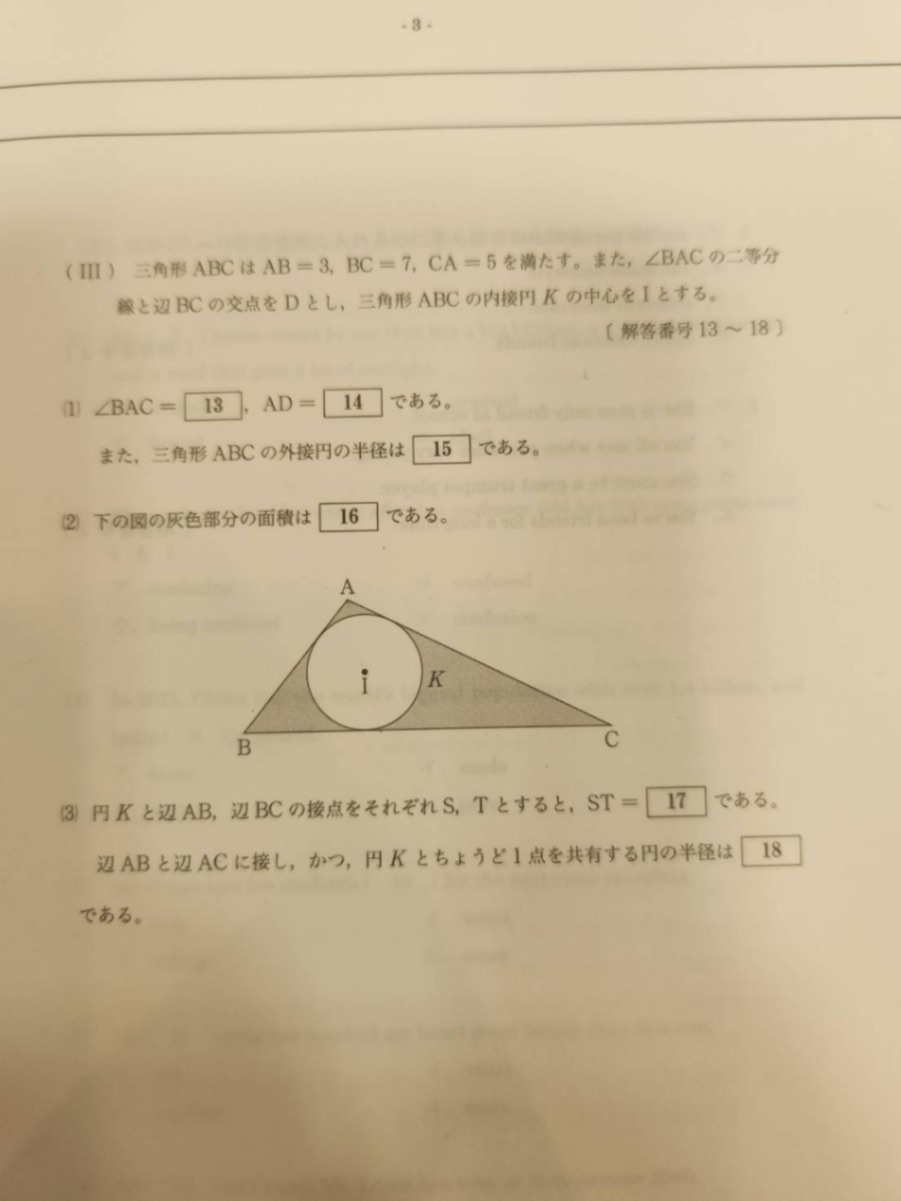
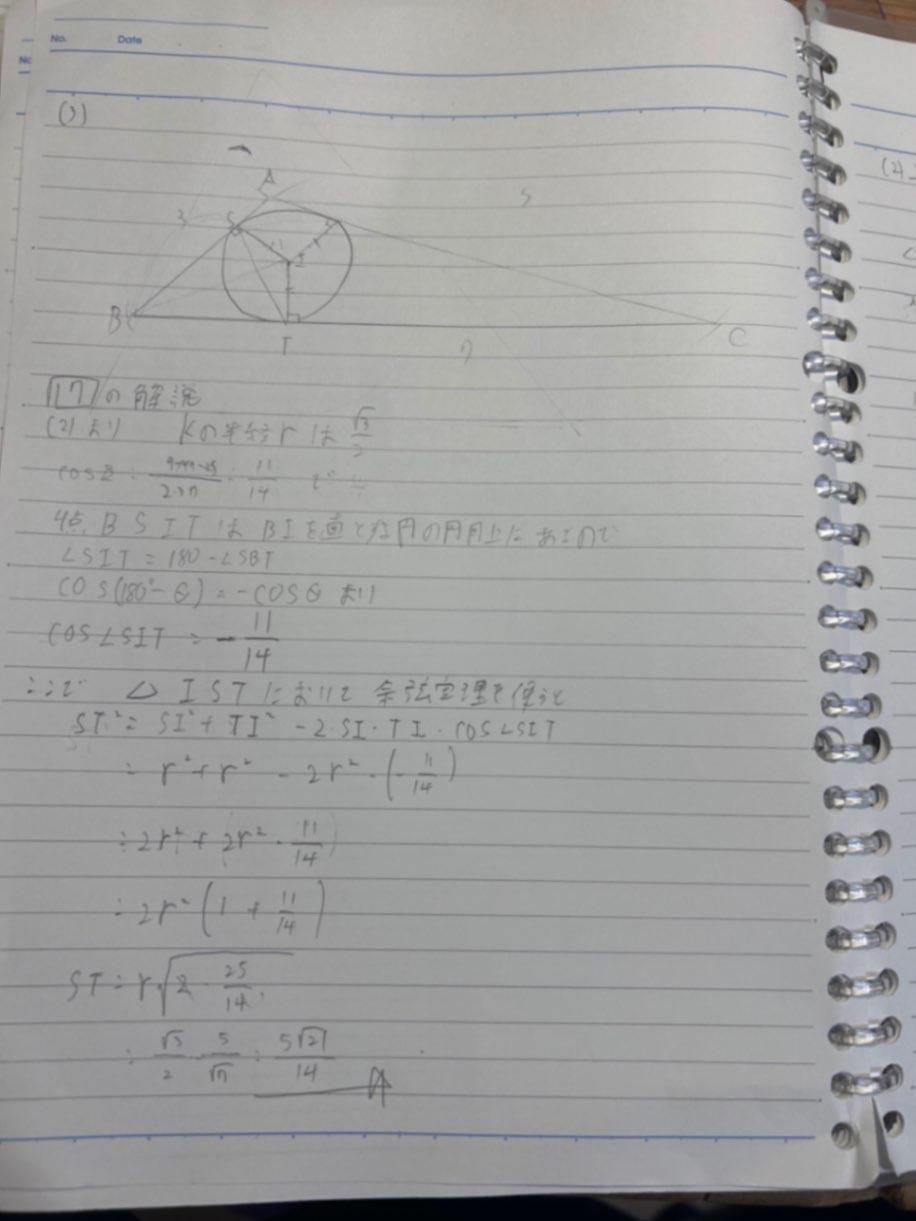
回答
この質問を今見つけましたが、もう閉店時間なので明日回答します。ゴメン。正解は持ってないのですか？13から17までのあなたの答を書いてくれるか、あなたのノートを写真でアップしてくれるといいのですか。お待ちしています。
あ、その図の中に30°60°の直角三角形は見えてますか？使えそうですから、見つけていなかったとしたら、もう少し考えておいてください。それで、もし解決したら、そのこともコメント欄で連絡してくださいね。
回答ありがとうございます! 正解は添付した一番下の写真の右上辺りに書きました。 30°60°の直角三角形は見えています。 今の方針はAMが分かれば解けるのでなんとかしてAMを求めようとしてるのですが中々求めれません。 現在わかってることは ・△SPIは1辺が√3/2の正三角形 ・ASとAPが1/2 ・∠SQPが150° ・△AOHが30°60°90°の直角三角形 ・SQ=SM=PQ=PH ・△MHOが△SPIと相似 ぐらいです。 △SQPを使ってSQを求めようとしましたがSQが1/2を超えてしまったので間違ってることはわかりました。 僕的には17で求めたSTを使うのかなとも考えましたがST使い方が思いつきませんでした。 解説を書いていただけるととても嬉しです。くさぼうぼうさんお願いします!