立体　切断

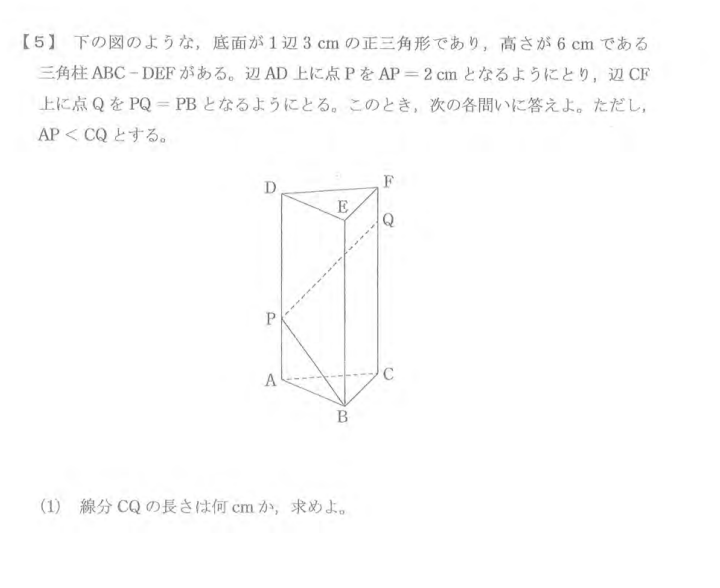
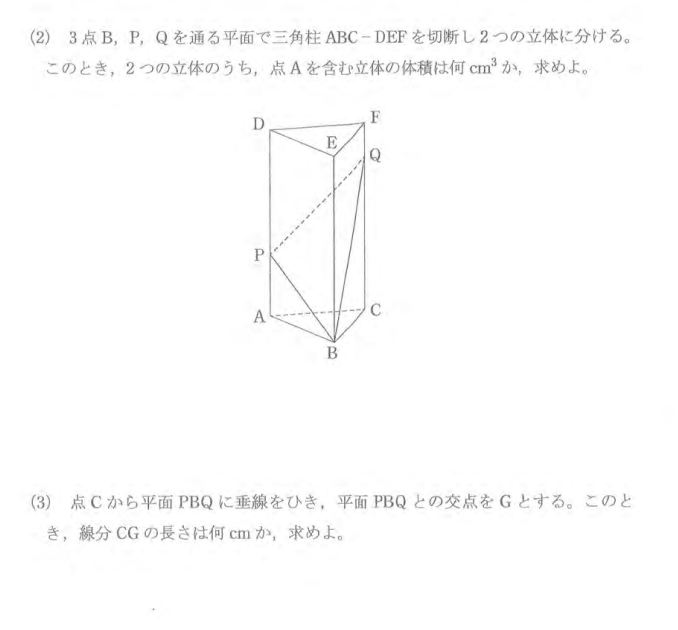
何度もすみません。この写真の問題も分かりませんでした。 （１）は４cm （２）は9√3／２ cm3　です。 （３）はけんとうもつきませんでした。

m nico さん、こんにちは。 毎回難問ばかりの質問で、焦っています。この質問の前のやつはいまだに見当がつきません。 この問題は、上のコメントに書いてしまいましたが、（２）の「Aを含む立体」は変な形で、それを平面PBC２切って2つにすれば、２つの三角錐に別れますよ。１つめは、頂点がPで底面がABCである三角錐。体積は $\dfrac{27\sqrt{3}}{2}$ です。もう一つの方は、頂点をP、底面をQBCと見ます。Pから平面ABCに下した垂線は、元の図の下から２ｃｍのところにある正三角形のPから対辺に下した垂線の長さですから $\dfrac{3\sqrt{3}}{2}$ で、垂線の足はちょうどBQの中点になっていますよ。この辺りは全体の図の中で確認してください。よって三角錐P-QBCの体積は $9\sqrt{3}$ 。 求める立体の体積は $\dfrac{27\sqrt{3}}{2}+9\sqrt{3}=\dfrac{27\sqrt{3}}{2}$ だと思うのですが。 （３）はその三角錐P-QBCを使います。体積は $9\sqrt{3}$と分かりました。三角形PQBの面積は出せますね。BQ=5だし、高さは先ほど求めた $\dfrac{3\sqrt{3}}{2}$ ですね。これで三角錐P-QBCの体積＝1/3△PQB×(Cから△PQBまでの高さ)。これで距離が出ますね。36/5かな？計算自体は保証しません(汗)！また、ここでの書き間違いなどもあるかもしれません。方針は分かってください。 こんな考え方でどうでしょうか？コメント欄になにか返事を書いてください。よろしく。