このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
極方程式
写真の問題（2）についてです。
自身の回答の仕方でも⚪︎でしょうか？
また、解答のHをどのように求めているのかが、分からないので解説していただきたいです。
お願いいたします。
【写真】
１枚目→問題
２枚目→自身のノート
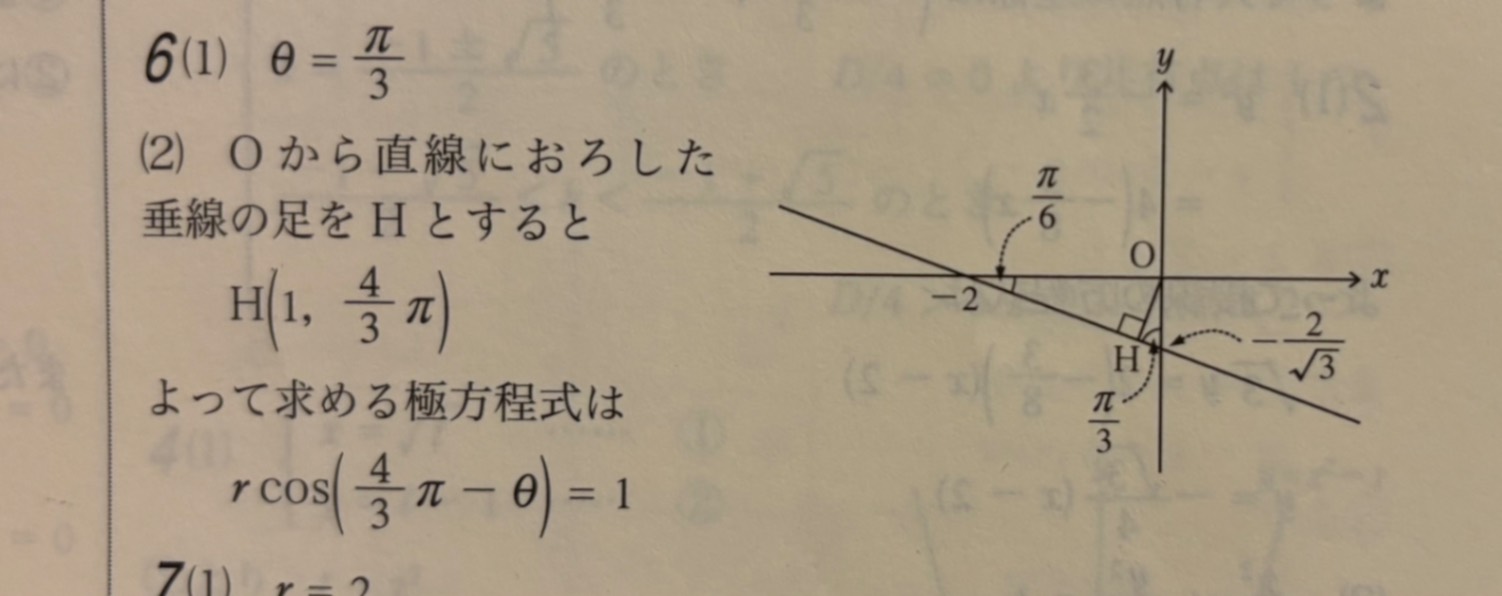
３枚目→解答、解説
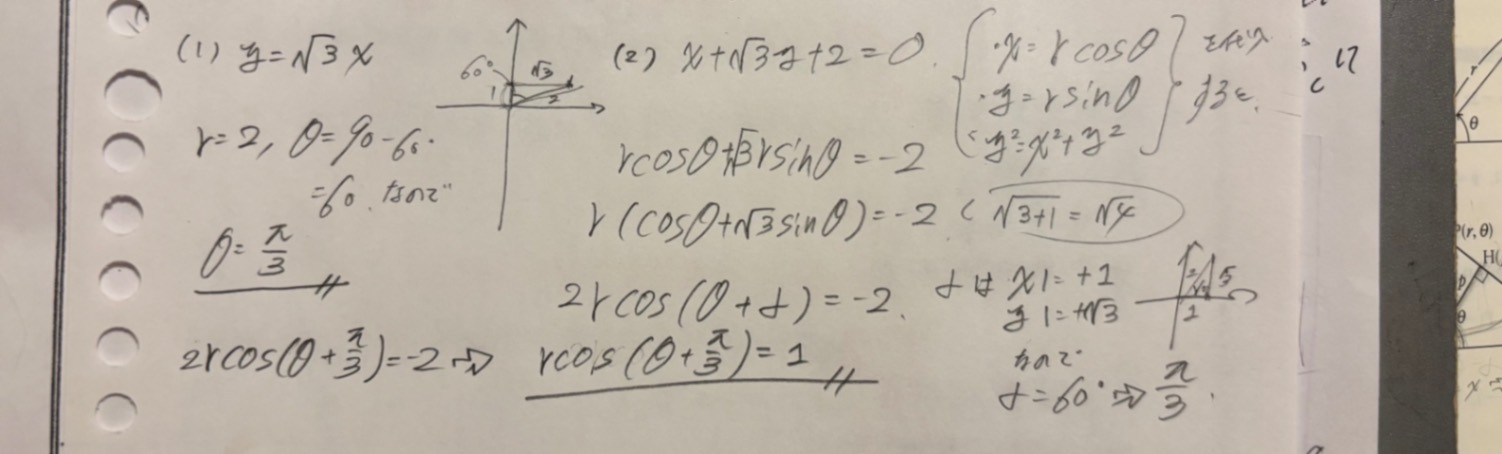
回答
ひなたさん、こんばんは。ちょっとお久しぶりですね。
まず点Hについて。
直線の傾きが $-\dfrac{1}{\sqrt{3}}$ ですから、直線とⅹ軸とのなす角をθとすると $\tan \theta =-\dfrac{1}{\sqrt{3}}$ ということです。ここからθ＝$\dfrac{5}{6} \pi$ が分かります。あとはその図のように角の大きさが分かっていきます。また直線と原点との距離を公式から求めれば１となりますので、極座標のｒは１、θは$\dfrac{4}{3} \pi-\theta$ が分かります。これで大丈夫ですか？
あなたの答案では、加法定理で普通はサインでやるところをコサインを使っていますね。それでもできるのですが、コサインの場合は＋αではなくーαになります。（コサインの加法定理を確認してください！）そこを直せば正解になります。おっと！右辺は１ではなくー１ですね！
見た目は正解と異なりますが、正解になりますよ。
これで大丈夫ですか？
=====================================
追記 2025/11/07 23:20～
$\cos\left(\dfrac{4}{3}\pi -\theta \right)$
$=\cos\left(-\dfrac{4}{3}\pi +\theta \right)$
$=-\cos\left(-\dfrac{4}{3}\pi +\theta +\pi \right)$
$=-\cos\left(\theta -\dfrac{\pi}{3}\pi \right)$
ですので、あなたの答も解答の答も同じです。
これで大丈夫ですか？
回答ありがとうございます。 解答の式が右辺＝1になっているのは何故なのでしょうか。
上の回答に追記しました。読んでください。
追記もありがとうございます。 その様に式変形して行けば良いのですね。 ですがまだ疑問が残っていまして、 θ＝5/6πが分かった後に作図してそのナス角の鋭角がπ/6になるところまでは分かったのですが、そこからどう計算したらHのθが4/3πになるのか、うまく導けませんでした。 理解力が乏しくお恥ずかしいのですが、また解説して下さると嬉しいです。
恥ずかしいなんて言ってたら大変ですよ！わからないことを質問するのは恥ずかしいことなんかではないので、どんどん聞いてください。 π/6までは分かったのですね。ｘ軸の交点ー２のところをＡとします。直角三角形ＯＡＨで、π/6ではない方の∠ＯＨＡはπ/3です。このときＨを極座標で表現すると、ＯＨ＝１，∠ｘＯＨ（左回転で測る）＝π＋π/3＝4/3πなのでＨ（１、4/3π）と書けます。 これで大丈夫ですか？