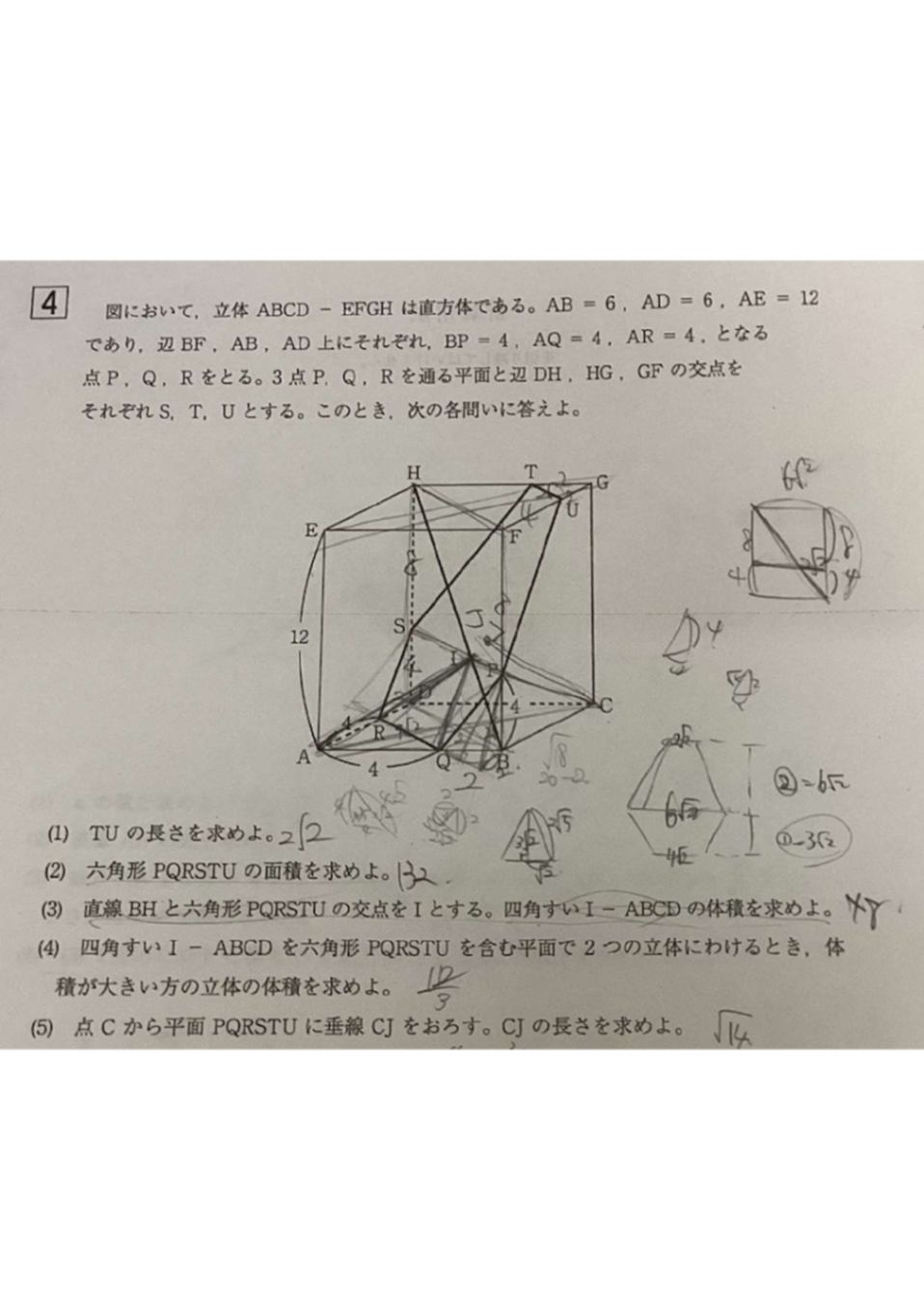
立体　切り分け

いつもすみません・・・。 （５）の問題がわかりませんでした。 （４）で求めた体積の値を使って求めるのでしょうか。

m nico さん、こんばんは。 （５）は体積がらみではないと思います。BとD,HとFがしれぞれ重なって見えるような方向から図を書きます。ついでにその図でCGを延長して、直線QPUの延長と交わる点をXとすれば、直角三角形△XQCの直角の頂点CからQXに下した垂線の長さがCJです。相似を使えばCJが求まります。 √14ではないような気がしますが… コメント欄になにか返事を書いてください。

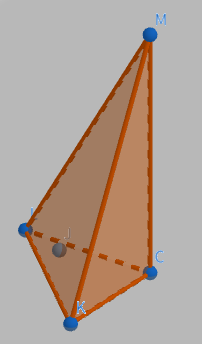
このサイトでの回答は初めてですが、お役に立てば幸いです。 細部は略して書きます。詳細が欲しいところがあればまた教えてください。 (2)は78、(4)は112/3だと思われます。 目標は垂線$\mathrm{CJ}$ですから、$\mathrm{CJ}$が高さになるような立体を見つけて、2通りの方法でその体積を表す方針で行きます。 ■解答１(誘導から外れる方法。直感的に分かりやすいかな？) 直線$\mathrm{PU,QR}$の交点を$\mathrm{K}$, 直線$\mathrm{QR,ST}$の交点を$\mathrm{L}$, 直線$\mathrm{QR,PU}$の交点を$\mathrm{M}$と置きます。 ここで三角錐$\mathrm{M-CKL}$に注目します。(1つ目の画像) この三角錐について、$\mathrm{CKL}$を底面とみると、体積$\mathrm{V}$は $$ \begin{align*} \mathrm{V} &= \frac{1}{3} \cdot \triangle \mathrm{CKL} \cdot \mathrm{CM}\\ &= \frac{1}{3} \cdot 32 \cdot 16 \end{align*} $$ と求められます。(この三角錐について調べる部分は全部省略しましたが、そこまで難しくないはずです) 一方、$\triangle \mathrm{MLK}$を底面とみると、 $$ \begin{align*} \mathrm{V} &= \frac{1}{3} \cdot \triangle \mathrm{KLM} \cdot \mathrm{CJ}\\ &= \frac{1}{3} \cdot 96 \cdot \mathrm{CJ} \end{align*} $$ と表せます。これらは等しいので、イコールで結んであげると、$\mathrm{CJ}=\frac{16}{3}$が導かれました。 ■解答２(誘導に乗る方法？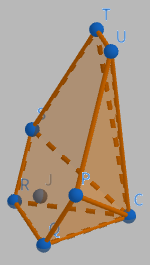) ・方針 まずは(4)をヒントに、直方体$\mathrm{ABCD-EFGH}$を平面$\mathrm{PQR}$で切り分けたうち、点$\mathrm{C}$を含む方の体積$\mathrm{V}$を求めます。次に、$\mathrm{V}$から余計な部分を引いて、六角錐$\mathrm{C-PQRSTU}$の体積$\mathrm{W}$を求めます(二つ目の画像は$\mathrm{W}$)。一方で、(2)で求めた面積とCJを使うと別の方法でWを表せますので、これで方程式を作れそうです。 ・解答 (4)では何をしたのかというと、四角錐$\mathrm{I-ABCD}$のうち、$\mathrm{V}$に入る部分の体積を求めました(下の面)。よって、同じことを他の５つの面でも行えば、それらの体積の和が$\mathrm{V}$となります。 一例として、四角錐$\mathrm{I-ABCD}$に関して、$\mathrm{V}$に入る部分の体積を求めてみましょう。((4)と同じことをしてます。) - 四角錐$\mathrm{I-ABCD}$のうち$\mathrm{V}$に入る部分、つまり五角錐$\mathrm{I-BCDRQ}$の体積を求めればよいです。 $$ \begin{align*} \text{五角錐}\mathrm{I-BCDRQ}\text{の体積} &= \frac{1}{3} \cdot (\text{五角形}\mathrm{BCDRQ}) \cdot (\text{高さ}) \\ &= \frac{1}{3} \cdot (36 - 8) \cdot 4 \\ &= \frac{112}{3} \end{align*} $$ となります。同じことをほかの5つの面に対しても行うと、 $$ \begin{align*} \mathrm{V} &= \text{下の面} + \text{手前の面} + \text{右の面} + \text{奥の面} + \text{左の面} + \text{上の面} \\ &= \frac{112}{3} + \frac{8}{3} + \frac{112}{3} + \frac{224}{3} + \frac{16}{3} + \frac{16}{3} \\ &= \frac{488}{3} \end{align*} $$ と、$\mathrm{V}$が求まりました(下の面以外の計算は略しました)。次に$\mathrm{W}$を求めます。 $$ \begin{align*} \mathrm{W} &= \mathrm{V} - (\text{三角錐}\mathrm{C-BPQ}) - (\text{三角錐}\mathrm{C-DRS}) - (\text{三角錐}\mathrm{C-GTU})\\ &= \frac{488}{3} - 8 - 8 - 8 \\ &= \frac{416}{3} \end{align*} $$ これで、六角錐$\mathrm{C-PQRSTU}$の体積$\mathrm{W}$が求まりました。今度は、底面を六角形$\mathrm{PQRSTU}$とみて$\mathrm{W}$を表してみます。 $$ \begin{align*} \mathrm{W} &= \frac{1}{3} \cdot (\text{六角形}\mathrm{PQRSTU}) \cdot \mathrm{CJ} \\ &= \frac{78}{3} \cdot \mathrm{CJ} \end{align*} $$ と表せます。これらは等しいので、イコールで結んであげると、$\mathrm{CJ}=\frac{16}{3}$が導かれました。