どこが間違っているのか教えてほしいです！

どこが間違っているのか教えてほしいです！

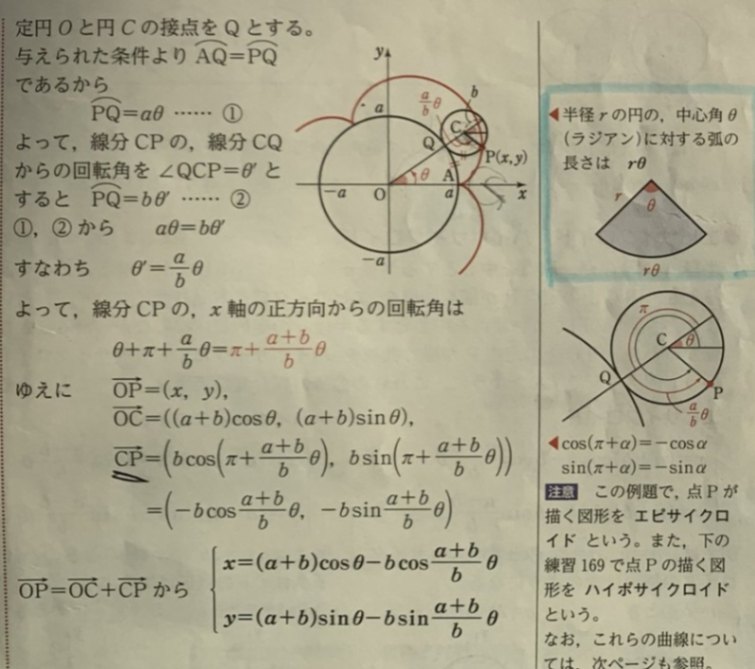
1枚目の写真の最後の2つの式が解答ですよね(^^) マカロンさんの答えは、xとyの媒介変数表示の最初に(a+b)とあります。恐らくここが間違っています。 解き直したら、出した式がどこの点を示しているのか、もう一度考えてみてくださいʘ⁠‿⁠ʘ また、解答に直接関係ないですが（もしかしたらテストとかで減点されるかもしれないけど）、モヤモヤするのでcos,sinの角度で(θ±π)や(θ±π/2)などがあれば変形しましょう。 cos(θ+π)= -cosθ sin(θ+π)= -sinθです。（他のも円周角を書けば分かりますヨ） 間違いの指摘しかしていません。どこか質問があれば聞いてみてください(⁠・⁠∀⁠・⁠) 追記 $\frac{(a+b)\theta}{b} + \pi$はあっています！ で、この角度がどこの辺と辺がなす角なのかが大事です。 ズバリ、線分CPとx軸正方向からの角度です。 え？線分CPとx軸は触れてないゾ？ 的な疑問が生まれるかもしれませんが、チャートの解答の図に、円Cの中心から、x軸正方向向かって平行に引いた線が見えます。その線と線分CPのなす角度は、x軸と線分CPのなす角度と同じになりますね？（わかりますか？）この考え方は後で出てきます。 じゃあ、この角度を出して何がしたいのか？ですが、点Pを表すために、今回はベクトル（成分表示）を用いています。円Oの中心から点P までの道順は、 点Oから点Cまで→点Cから点Pまで の順です。 点Oから点Cまでは、θと2つの円の半径を用いて簡単に表せます。 ベクトルOC$(a+b)cosθ,(a+b)sinθ$　です 点Cから点Pまでを表すために、$\frac{(a+b)\theta}{b} + \pi$を用います。 ここでの$ポイント$は、点Cを座標平面の原点だと、とらえ直すことです。（後で出て来ると言ったやつ） 点Cから点Pまで表す ベクトルCP${(b)cos(\frac{(a+b)\theta}{b} + \pi),(b)sin(\frac{(a+b)\theta}{b} + \pi)}$ 色々ゴチャゴチャしてきたので、まとめます。 1：点Pの座標をθを用いて表したい。 2：点Pを表すために、ベクトルを使う 3：点Oから点Pまで、直接表すのは難しい 4：まず、点Oから点Cまでを表そう（θと半径a,bだけで表せる！） 5：点Cから点Pまでを表したい 6：$点Cを新たに座標平面の原点だと捉え直す。$すると、新しい座標平面のx軸と、線分CPのなす角が分かる 7：その角度と円Cの半径bを用いれば点Cから点Pまでをベクトルて表せる 8：作った2つのベクトル（点Oから点Cまでと、点Cから点Pまでの2つ）を足す ⇛a,b,θだけを使って表せる 長くなってすいません