このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
共テ1a 図形と計量
(1)について、自由に変えることのできる三角形acpについて考えると言うことはわかったのですが、それ以降の絞り方がわかりません。答えは0と2でした。
回答
共通テスト、私は嫌いですಠ_ಠ
そんなことは置いといて、
あまり理論的な解説ができないかもしれません。すいません。
0:これを満たすときに示せることは、BCが直径で、点Pがその円上にある。ということでしょうか(こじつけかも)。△ACPが最大になるとは言えない気がします。気がする。。実際に図を描いてみると、△ACPがとても小さいとわかると思う。
2:これを満たすことは、図形的に不可能かな?0番にも言えることですが(多分)、今回の三角形が、鋭角三角形か鈍角三角形のどちらかわかりますか?
一番長い辺とその他の辺の関係でわかりますが。
言ってしまうと、
△ABCは鈍角三角形です。即ち、△ABCは、外接円の中心を三角形の内部に持ちません。そう考えるとBPがOの直径になるのは、Pの位置の条件に反しませんか?
△ABCが鈍角三角形で、外接円と、中心との位置関係を再確認してから、もう一度考えてみると良いかもしれません。
1:イメージしてみると、、分かるかな
上手く文章で説明するのが難しいです。
私は共テで考察系(そう勝手に呼んでます。正しい文章を選べだとか、当てはまる文章を選べたとか)の問題が出てきたら、一旦飛ばして最後に考えるようにしてます。時間がかかることは後回し!
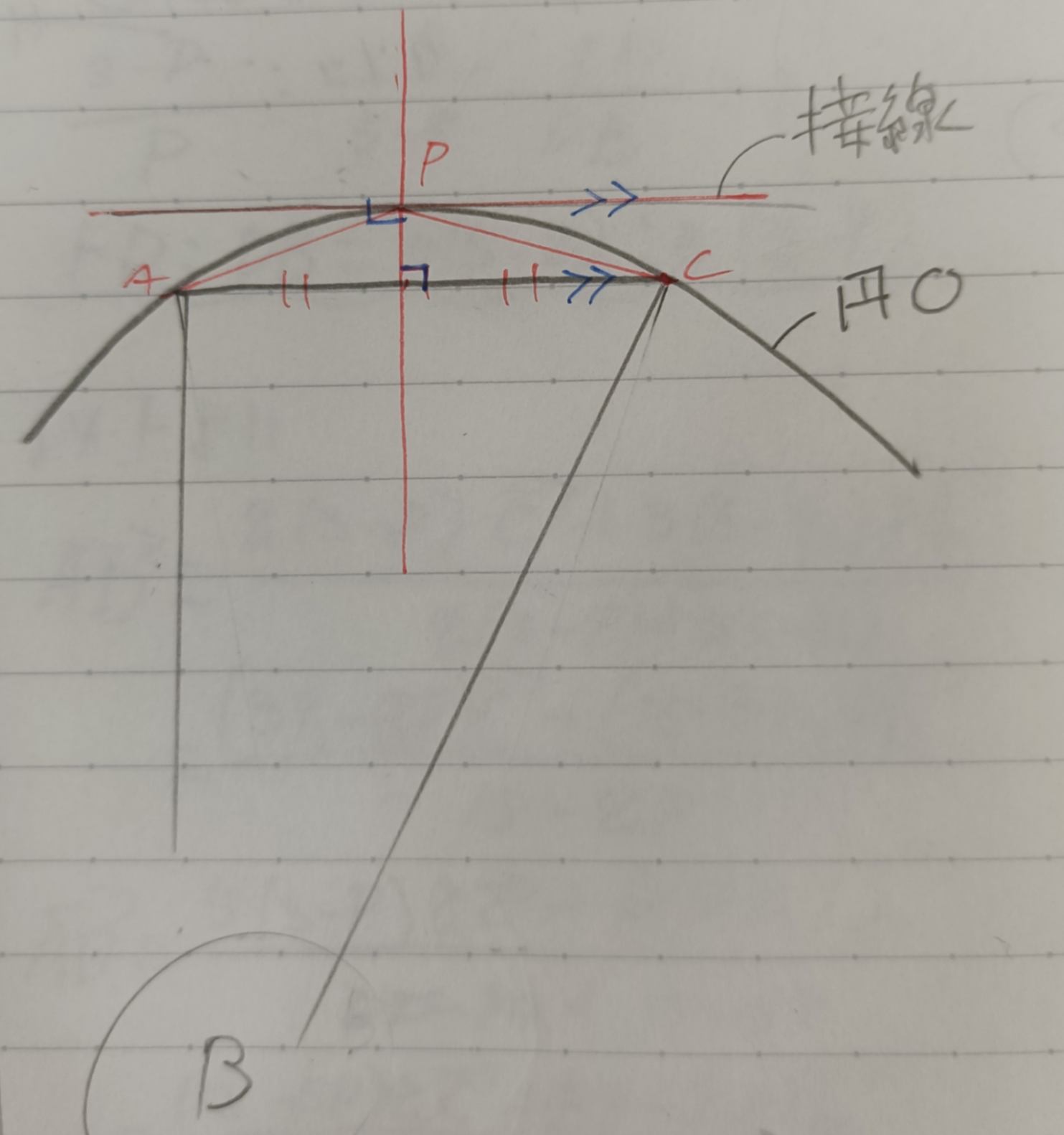
この写真から△ACPが最大になるにはAP=CPの二等辺三角形である(1)。点Pの接線と辺ACが平行(4)だと分かるかな?底辺が決められた三角形の面積を最大にするには、高さを最大にする必要があるため。
この写真だと∠CABが直角に見えるけど、違います。
教えてくださってありがとうございます。確かに図を見たらそうだなあと納得できました。 でも、きっちり自分で理論立てて解けそうにないです泣 共テで出てきたらほかの問題で点数を取る方が賢いですかね...
共テは時間との勝負ですもんね。とにかく解ける問題を全て解けるようにスタスタいきましょう!
まかろん さん、こんばんは。
△ABCの形状がどうであれ、四角形ABCPの面積のうち、△ABCの部分はもう決まっているので、△CPAの面積だけを考えればいいですね。
△CPAは辺CAは決まっているので、面積を決めるのは高さだけです。Pから辺CAに引いた垂線の長さが高さですから、垂線の長さが一番長くなる点が求めるPの位置です。つまりPはCAから一番盛り上がっているところ、すなわち弧CAの中点ですよ。このことが分かってから⓪から④までを読めば、どれが正しくてどれが違っているか分かりますよ。③は円周角の定理「長さの等しい弧に対する円周角は等しい」で正しいことが分かります。
これで大丈夫ですか?下のコメント欄になにか返事を書いてください。
教えてくださってありがとうございます。 納得できました!!③の説明もわかりました!
どういたしまして。またどうぞ。