このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
証明
52の( 2)です
考えたんですけど、わかりませんでした😭
一応、円周角の定理の逆を使って証明したいと思い、角fde 角角daf を示そうと思いました。でも、できませんでした。ヒントいただけませんか?
そもそも方針が違ってますか??😭

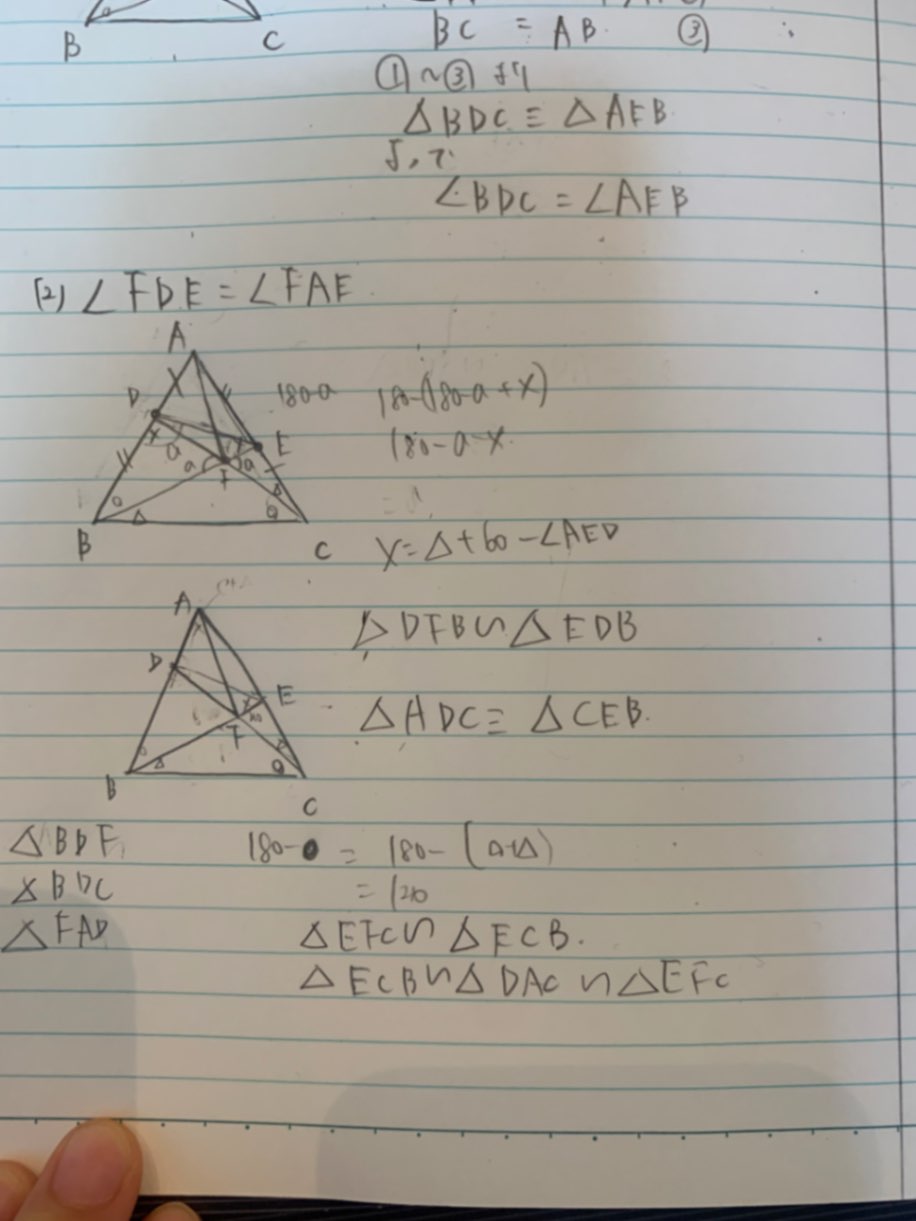
回答
百花さん、おはようございます!
円周角を利用しようというのはいい手ですね。
問題の答から逆にたどっていって考える方法ですね。
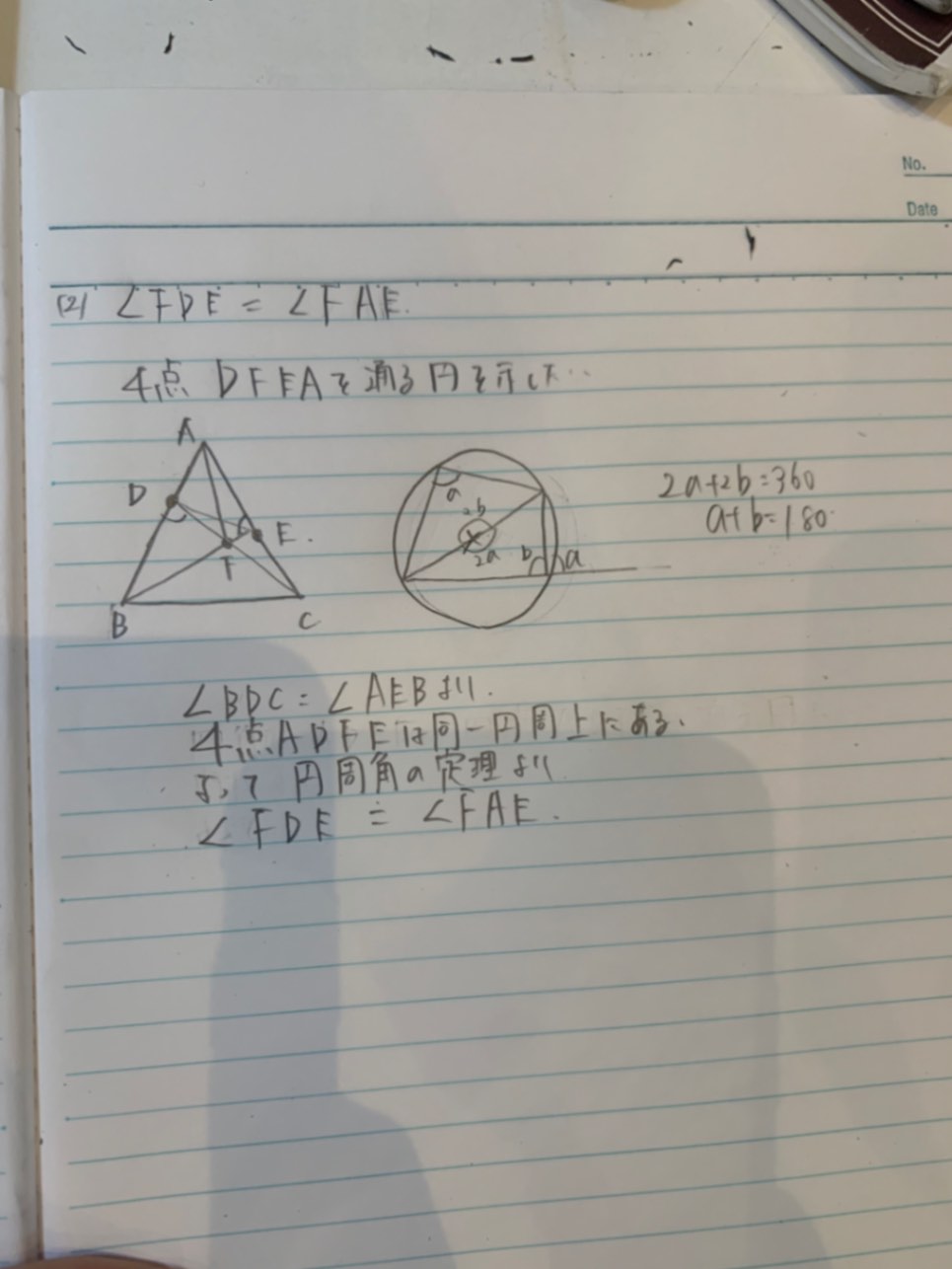
∠FDE=∠DAEを示したい
この2つの角は辺FEを共有してるので、弧FEが考えられれば円周角の定理で示せそう
となると、4点DFEAを通る円の存在を示さねば。
あ!!(1)が使えるんだ。(1)は(2)の誘導だったんだぁ!
さて、これでどうでしょう。
考えてみて、納得できれば証明も書いてみてください。
結果報告お待ちしています。
多分できました!
あはは…ずいぶんさっぱりした証明です!根拠は日本語でも書きましょう。ちゃんと四角形DFEAにおいて、外角とその内対角が等しいからとか、対角の和が180°だからくらいは書いたほうがいいですよ。
なるほど、、証明の書き方忘れてしまいました笑 ちゃんと書き直してみます!
じゃ、がんばって👏