このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
図形

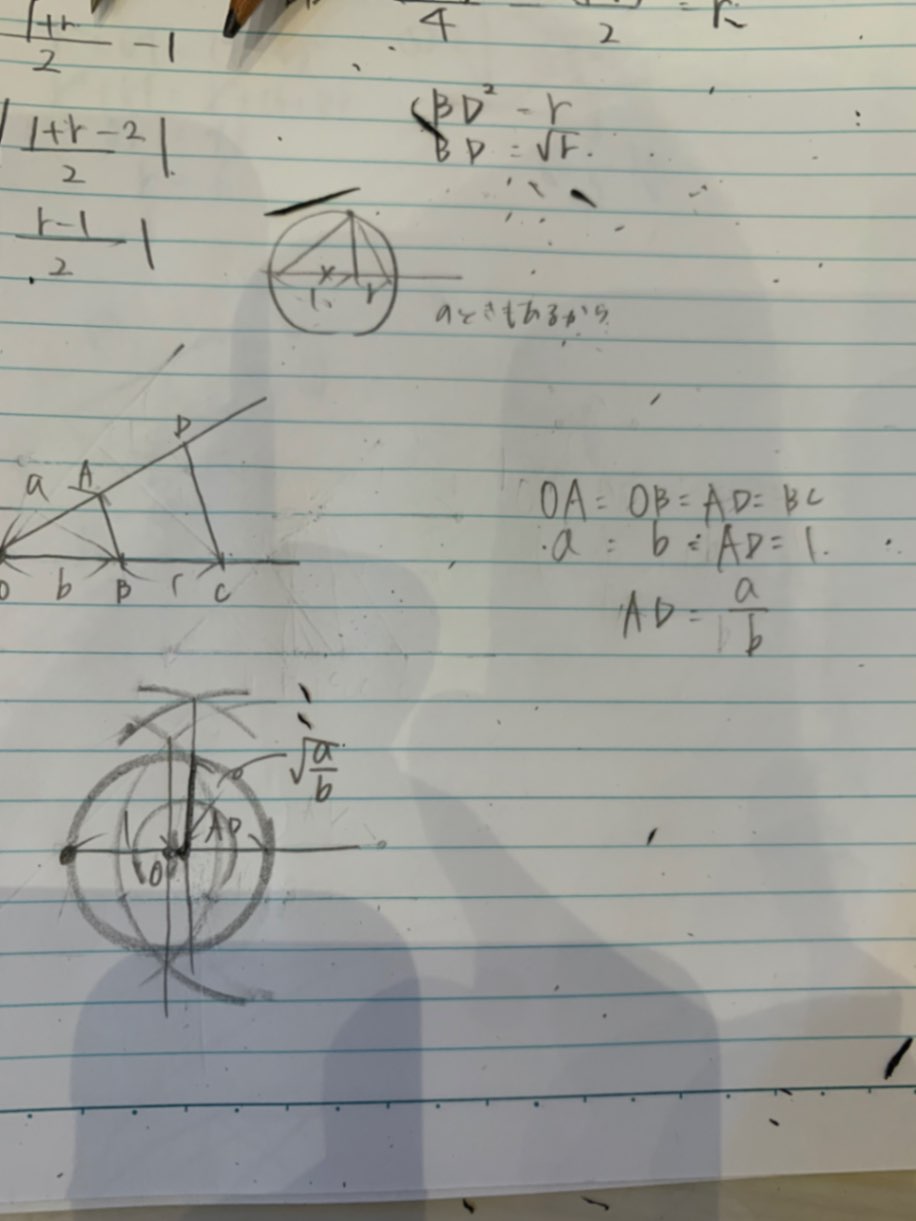


回答
ありがとうございます🙏 平方根の作図ってどうやってやるんですか??わかりません💦
作図してみたのですがあってますか?? まず直線を引いて、そこに上の図から1のA Dの長さを写しとる 次に中心を垂直二等分線を引いて求め、円をかく 最後にA Dの左端への垂線を引く みたいな感じでやりました。 調べてやったので、なんで平方根の作図ができるのかはわかりません。 (ヒントいただけたら嬉しいです🙏)
https://mathq2nd.com/webapp/thread/detail/3811/ ←あなたの昔の質問です!平方根の作図で検索したら見つかりました! √aが欲しかったら、aの長さと1を足した長さの線分を直径とする円を描き、aと1のつなぎ目のところから直径に垂直な線をひく。 その直線の円との交点までの長さが√a。これは三角形の相似から分かりますよ。 今の問題ならば、a/bを作図で求めたら、それを1だけ延長して、それを直径とする円を考えましょう。 これでどうでしょう。
ありがとうございます! a/bを作図で求めたら、それを1だけ延長して、それを直径とする円を考えましょう。 わざわざ写しとる必要はないんですね💦 三角形の相似で証明できるんですか?
55もやってみました!考え方あっていますか?
私も解答・解説が充実したフォーカスゴールドで勉強したいのですが、学校の宿題でして、、 略解は配られてるんですけど、解説がなくて困ってます💦 予習していかないと授業についていけないもので、、
55について。 eとvがおかしいかな。 20カ所の頂点を切りました。1つの頂点の切断について考えると 面は1個増えます。 辺は3本増えます。 頂点は3個出来て1個なくなるので2個増えます。 という分けて、新しい立体の f=もともと12面+1面増加×20カ所=32 e=もともと30本+3本増加×20カ所=90 v=もともと20個+(3個増加ー1個なくなる)×20カ所=60 オイラーの多面体定理v-e+f=2が成り立ちます。 これでわかりますか?疑問点はさらにコメント欄で。
配られた答えた少し違うのですが、もしかして解答が間違ってますか??
いや、私の方が間違ってるかも。あ!わかりました。角を切り取るときの切り方ですが私は単に「角をちょっと切り落とす」と理解してましたが、図をよ~く見ると、辺の半分まで切っちゃうのですね。もともとあった辺はなくなるということですね。それならあなたの出会っているのですね。失礼しました!!(問題の文章が不完全だぁ!)
あ、不完全ではなかったです。私が「各辺の中点…」を見逃していました。ゴメンナサイ!
ありがとうございます💗 空間図形は難しいですね、、 問題に正十二面体が書いてあったから、少しはイメージできたんですが、図がなければそもそも正十二面体がどのような形をしているかわかりませんでした。 ある程度の図形は覚えておくべきですか?😯
そうですねぇ、覚えた方がいいと思いますよ。といっても、辺や頂点の数は不要です。正何面体を作る面が正何角形なのかだけでいいです。図なして正多面体の問題は出ることはあります。ネットから図をひろってきて印刷して、目につくところにでも貼っておいたらどうでしょう。