このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
積分
写真のノート内にある緑🟢に書いてある疑問について教えて頂きたいです。
∮0→2で考えたのはノート下部にあるようにG(x)を微分=0を解いたところから持ってきました。
【写真】
1.2枚目→問題
3枚目→自身のノート

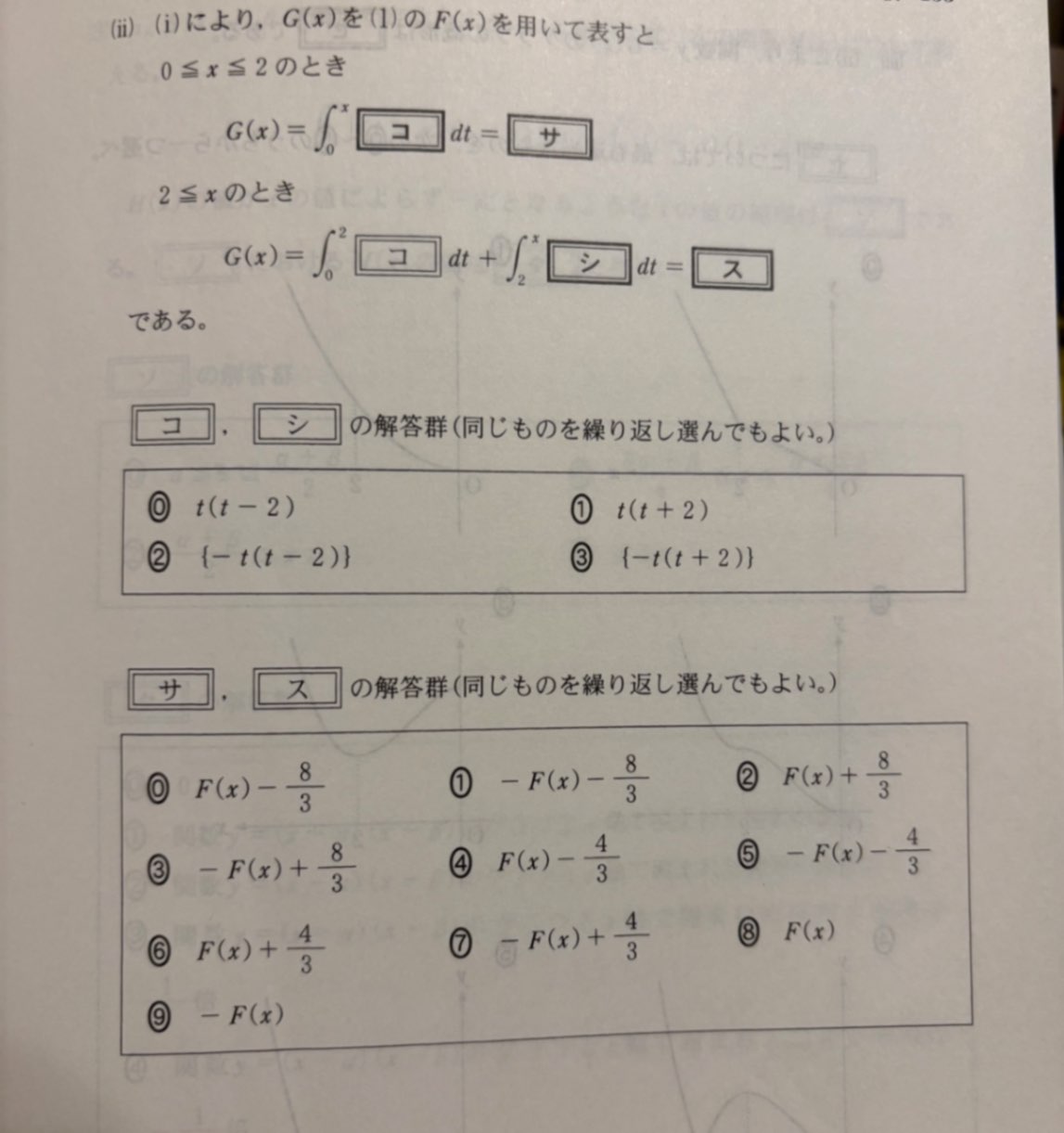

回答
ひなたさん、こんばんは。
ちょっと質問個所がわからないのですが。
緑で書いてある中カッコのところですか?
そこの「当てはめてよい」理由を聞いていますか?
なぜ9ではいけないのかっていうところですか?これが緑のマルかな?
どの部分が9だと考えている?それが分かりません。
これからちょっと受験生と11時まで付き合わなければならず、わるけど回答は明日になります。
質問個所、内容が分かるよう、ちょっと書き添えておいてください。
緑とか青がはっきりしないので、質問はなるべくテキストでお願いします。
==================
追記 2026/01/15 10:30~
コメント拝見しました。
あらためてあなたの(ii)①の部分の答案を読みましたが、意図が分かりませんでした。
0≦x≦2の範囲ですよね。
そもそもxは2を超えてないので、単に0からxまでの定積分でいいので、それはG(x)そのものですね。0から2までの定積分って関係ないですよね。
中カッコの青?字の部分は、ケから当然のことです。
これで大丈夫ですか?
あまり答になってないかな?
「分からないのはここです!!」とさらに示してくれれば答えますよ。
分かりづらくてすみません🙇 9ではなく↑(上矢印)で書いてます。 「サ」の解答が何故こう考えてはいけないのかが分かりませんでした。
書き間違いで「サ」が2つになってしまっているのですが、間違えている方の「サ」です。 ややこしくてすみません😭
回答ありがとうございます。 範囲が指定されているからといってその期間で積分するわけではないのですね?
はい。もともとの定積分は「0からxまでやりなさい」という記号です。 でも積分の終点であるxの値によって(具体的にはxが2より大きいか小さいかによって)絶対値を外した形の被積分関数が異なるので、x≧2の時は積分範囲を2つ(0から2と2からx)に分けて、それぞれの場合の被積分関数を積分しなければなりません。 大丈夫かな?
成る程! 納得しました。ありがとうございます😊
大丈夫ですか?またどうぞ。