このサイトはお使いのブラウザでは正常に動作しません。Google Chromeなど、別のブラウザを使用してください。
積分
写真の問題(3)についてです。
∮の連結を考えて解いたら=0になってしまったのですが、解答を見たところ
範囲が「α≦x≦β」の所は理解出来るのですが、
「x≧α」と「β≦x」の式が何故そのようになるのかがわかりませんでした。
解説お願い致します。
【写真】
I枚目→問題
2枚目→解答
3枚目→自身のノート
(追記: 2026年1月18日8:28)
【追加写真】
4.5枚目
(追記: 2026年1月18日8:29)
解き直した写真追加しました。





回答
ひなたさん、こんにちは。回答が遅れてゴメン。
書き直しました(2026/01/16 09:50)
模範解答の(3)の冒頭が変ですね。
問題文でx≧αと制限がついているので、(3)で改めてそんなことを書く必要はないですよね。
それをわざわざ書いているので、「x≧α」が場合分けの1つみたいに誤解したのでは?
あなたが質問で書いている「「x≧α」と「β≦x」の式」というとらえ方はおかしいのです。
気持ちとしては「x≧αは大前提」「場合分けは(i)α≦x≦βの場合(ii)α≦β≦xの場合」です。
ただ問題文にα<βとありますから、α≦β≦xと書く必要はないので「β≦xの場合」となっています。
模範解答の(3)の3行目は単に問題の関数をそのまま書いてみただけです。これもなくていいですね。
読み込まねばならないのはこのあとです。
大事なのは、もともとの範囲である「x≧α」という範囲を2つに別けたことです。
そのxがβより小さい場合と大きい場合では、絶対値を外したときの被積分関数が異なります。
場合その1)α≦x≦βのときは絶対値を外すとマイナスが出てきて、全体は(3)の7行目まで簡単にできました。
場合その2)もう一つの場合分けとしてxがβを超えたβ≦xの範囲で調べています。
この解答のやりかたは、H(x)の前半の定積分での被積分関数がβの前後で異なるので、
(H(X)=の式)積分をαからβまでとβからxまでに分けました。H(x)の後半は絶対値は付いていないので被積分関数はかわらず、そのままαからxまでの定積分でいいです。
それ以降の変形は読んで納得できますか?
あなたの答案の場合分けの条件がおかしいです。
絶対値が付いた式の正負ではないです。
絶対値が付かない(t-α)(t-β)の正負でわけるのなら分かります。
(t-α)(t-β)≧0とt≦α、β≦tとは同じことで、さらにtはαからxまで変化しますので、その終点のt=xがこの範囲にあるかどうかで1つの場合になります。つまりx≦α、β≦xの場合です。もっともx≦αは問題文でないことが分かっていますので、「β≦xの場合」になります。
同様に(t-α)(t-β)≦0とα≦t≦βは同じことです。tでの積分の終点であるt=xがこの範囲にある場合がもう一つの場合分けです。
最後の行とその前の行はどういう考えで作った式なのかよくわかりません。
aからxまでの積分とxからaまでの積分はおかしいです。
もう一度、場合分けとその時の被積分関数を慎重に考えてみて。
α≦x≦βの場合では前半の積分の絶対値をとってマイナスにするだけで計算が進められます。
β≦xの場合はtがαからβまでの積分とtがβからxまでの積分とに別けなければならないですね。
tがαからβまでの積分は前半の積分の絶対値をとってマイナスにして、tがβからxまでの積分は単に絶対値を外しただけで計算です。
これで大丈夫ですか?
今時間がないのであとで私のおすすめを書きます。
(追記: 2026年1月16日17:34)
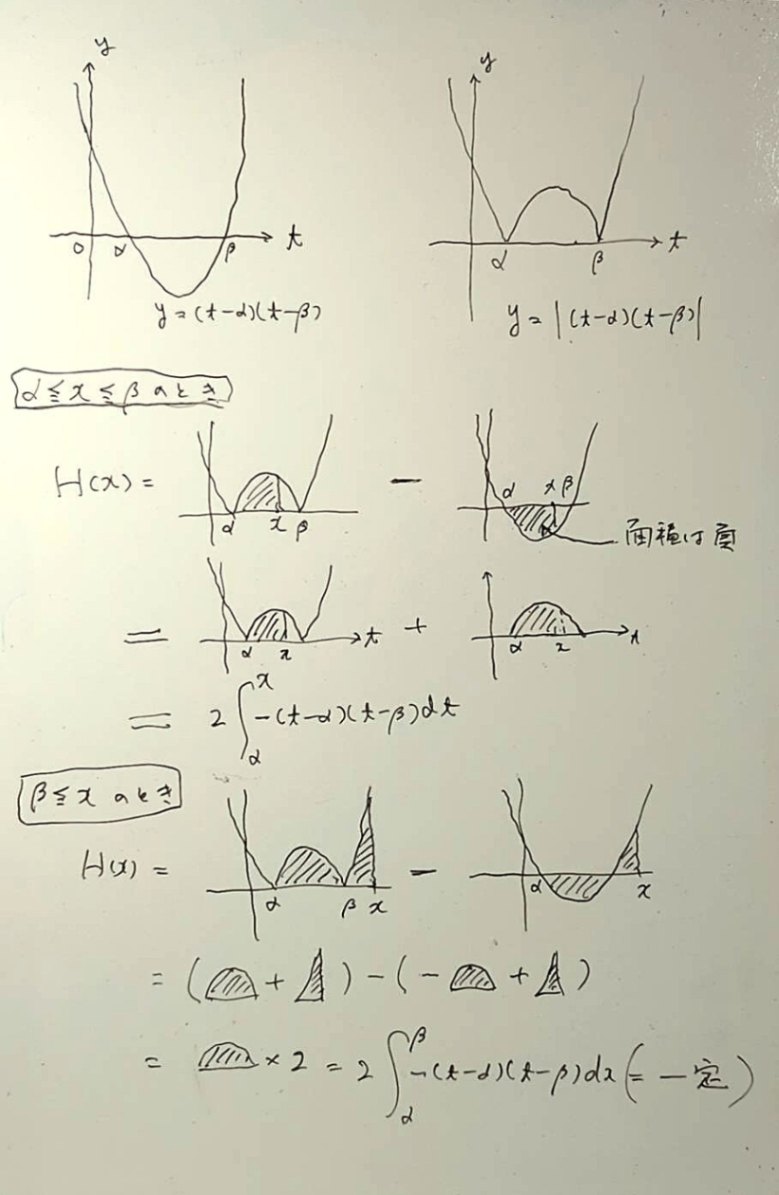
言葉では大変なので、図をアップしました。
tで積分ですから横軸はtです。
xは積分の終点です。
xがβより大きいか小さいかで積分の中味が変わります。
場合分けの意味は図のようになります。
これでどうですか?
対面でなく教えるのって難しいです。
回答ありがとうございます。 範囲を2つに分けたのは「x≧β」ですか?
ごめんなさい。最近謝ることが多くて反省してます! いま見返したら、私の回答が変でした。 これから書き換えます。
丁寧な解説感謝いたします🙇 今は見返す時間が無いので、後でまた確認してコメントします。
図解まで下さりありがとうございます。 ノートの写真追加したので考え方のプロセスが合ってるか確認してくださると嬉しいです。 (4枚目と5枚目の写真は順番上下逆になってしまいました。見づらくてすみません🙇)
ノートの写真、拝見しました。 それで大丈夫ですね。積分区間のひっくり返しとかマイナスの処理とか、ちょっと曲芸っぽいですが(笑)大丈夫です。
確認して下さりありがとうございます、助かりました🙇